不平衡資料的二元分類 1：選擇正確的衡量指標

不平衡資料 (Imbalanced Data) 在二元分類中是一大難題，卻也是最常見的情境。比如說，如果寄送行銷簡訊給一個消費者，他會不會回覆？一筆信用卡刷卡交易是不是盜刷？一個地區在一個時間點會不會發生搶案？這些問題，大部分的情況下都是陰性 (Negative，如：沒有回覆、不是盜刷、沒有搶案等)，只有極少的比率 (可能 < 1%) 是陽性，這種情況就叫做「不平衡資料」。最近不論是工作上或是自己做的 side project，都時常遇到資料不平衡的情況，因此想跟大家聊聊怎麼處理不平衡資料的分類問題。

準確度悖論：為什麼不能用準確度當作分類好壞的衡量指標？

在不平衡資料的分類問題中，如果我們使用「準確度」(Accuracy) 作為模型好壞的主要衡量指標，會遇到所謂「準確度悖論」的問題：假設盜刷交易佔總交易數的 0.5%，非盜刷交易佔總交易數的 99.5%。這時如果我們直接說：所有交易都不是盜刷，就可以得到準確度為 99.5% 的模型。儘管這個模型完全無法找出哪些交易是盜刷交易，但要另外建立一個超級準 (準確度 99.99%) 的機器學習模型，好像也不大實際。我們稱這樣的情況作「準確度悖論 (Accuracy Paradox) 」— 準確度不代表模型的好壞。

常見的衡量指標：分類錯誤成本

因此，在不平衡資料的分類問題中，我們更常採用其他的評估方法，比如說：曲線下面積 (Area under Curve, AUC) 與 F-指標 (F-measure)。在開始介紹這兩項指標前，我們要先理解分類模型中很重要的衡量機制：模糊矩陣 (Confusion Matrix)，如下圖所示：

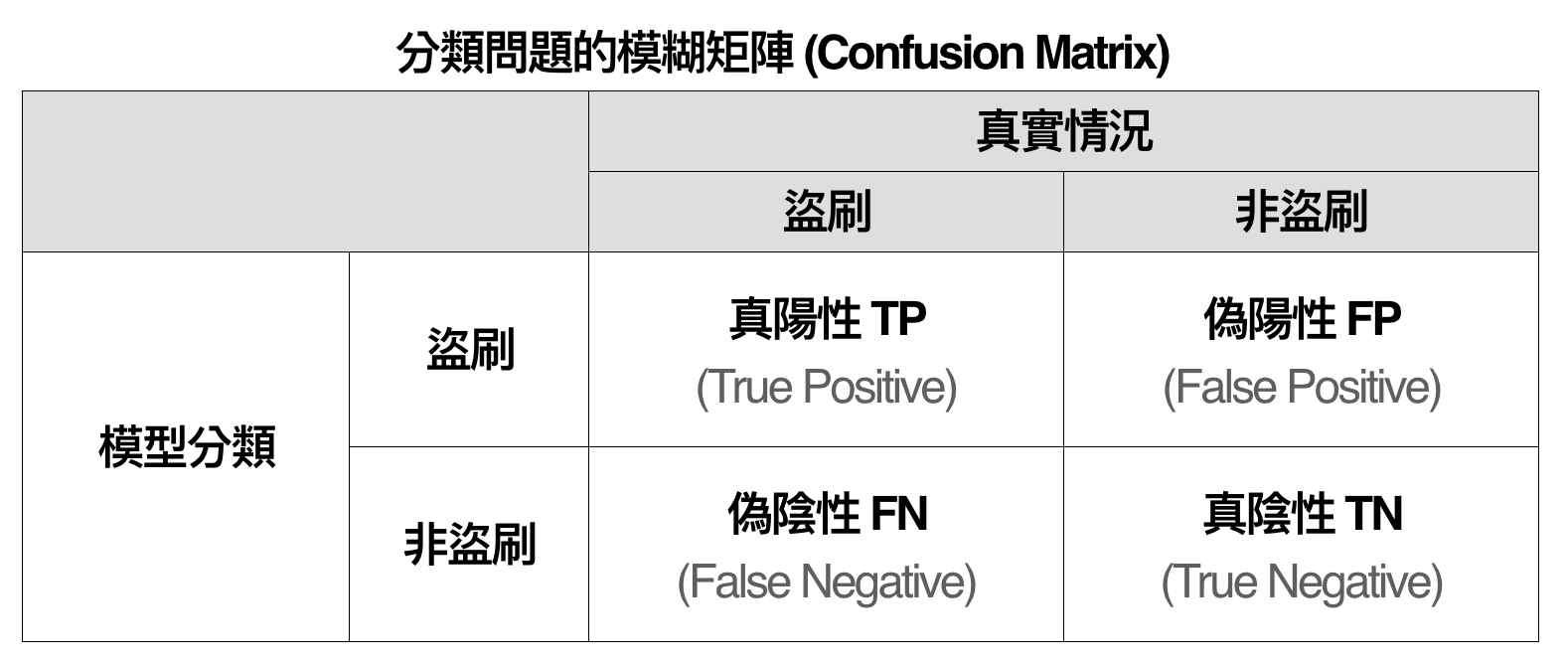
其中矩陣的每個格子是填入個體的數量，比如說：TP = 實際為盜刷，且被模型分類為盜刷的交易數，以此類推。前面有提到，準確度在不平衡類別的分類問題時不是個好的指標。因此，假設我們有很好的領域知識，比如說：如果信用卡被盜刷但我們沒有立刻阻止，公司會要花至少 50,000 元的處理成本；如果是正常交易但我們阻止交易的話，需要花 100 元的處理成本。我們定義 C(1, 0) 為誤把陽性個體分類成陰性的成本，C(0, 1) 為誤把陰性個體分類成陽性的成本，此時 $latex C(1, 0) = 50000$ 而 C(0, 1) = 100。如此一來，我們可以衡量分類錯誤的總成本：C(1, 0) * FN + C(0, 1) * FP，這樣的指標更能衡量分類模型經濟效益上的好壞。

常見的衡量指標：ROC 曲線 / AUC

如果實際上的成本很難估計的話，我們也有一些統計量可以幫我們更客觀的衡量不平衡資料下二元分類模型的好壞。由模糊矩陣出發，我們可以定義出以下幾個很重要的指標：

• 準確度 (Accuracy) = (TP + TN) / (TP + FP + TN + FN)，代表個體被分類正確之比率
• 召回度 (Recall) = TP / (TP + FN)，代表在所有實際為陽性的個體中，被正確判斷為陽性之比率
• 明確度 (Specificity) = TN / (TN + FP)，在所有實際為陰性的個體中，被正確判斷為陰性之比率
• 精確度 (Precision) = TP / (TP + FP)，代表在所有被正確判斷為陽性的個體中，確實為陽性之比率

上面這些指標其實彼此間互有關係。首先，我們可以來探討 Recall 跟 1 – Specificity 間的關係。當 Recall = 1 的時候，代表所有為陽性的個體都被正確分類為陽性，這時很有可能我們將「所有個體」都當成陽性 (也就是分類模型的門檻機率 = 1)，這時所有陰性個體都被分錯了，使得 1 – Specifity = 1 – 0 = 1。反之，Recall = 0 的時候，代表所有為陽性的個體都被錯誤分類為陰性 (也就是分類模型的門檻機率 = 0)，這時很有可能我們將「所有個體」都當成陰性，這時所有陰性個體都被分對了，使得 1 – Specifity = 1 – 1 = 0。所以我們可以知道， 1- Specificity 跟 Recall 其實存在正向關係。如果我們以 1 – Specifity 作 x 軸，Recall 作 y 軸，繪製不同門檻機率時兩個指標的數值，就可以得到ROC 曲線 (Receiver Operating Characteristic Curve) ，如下圖所示。

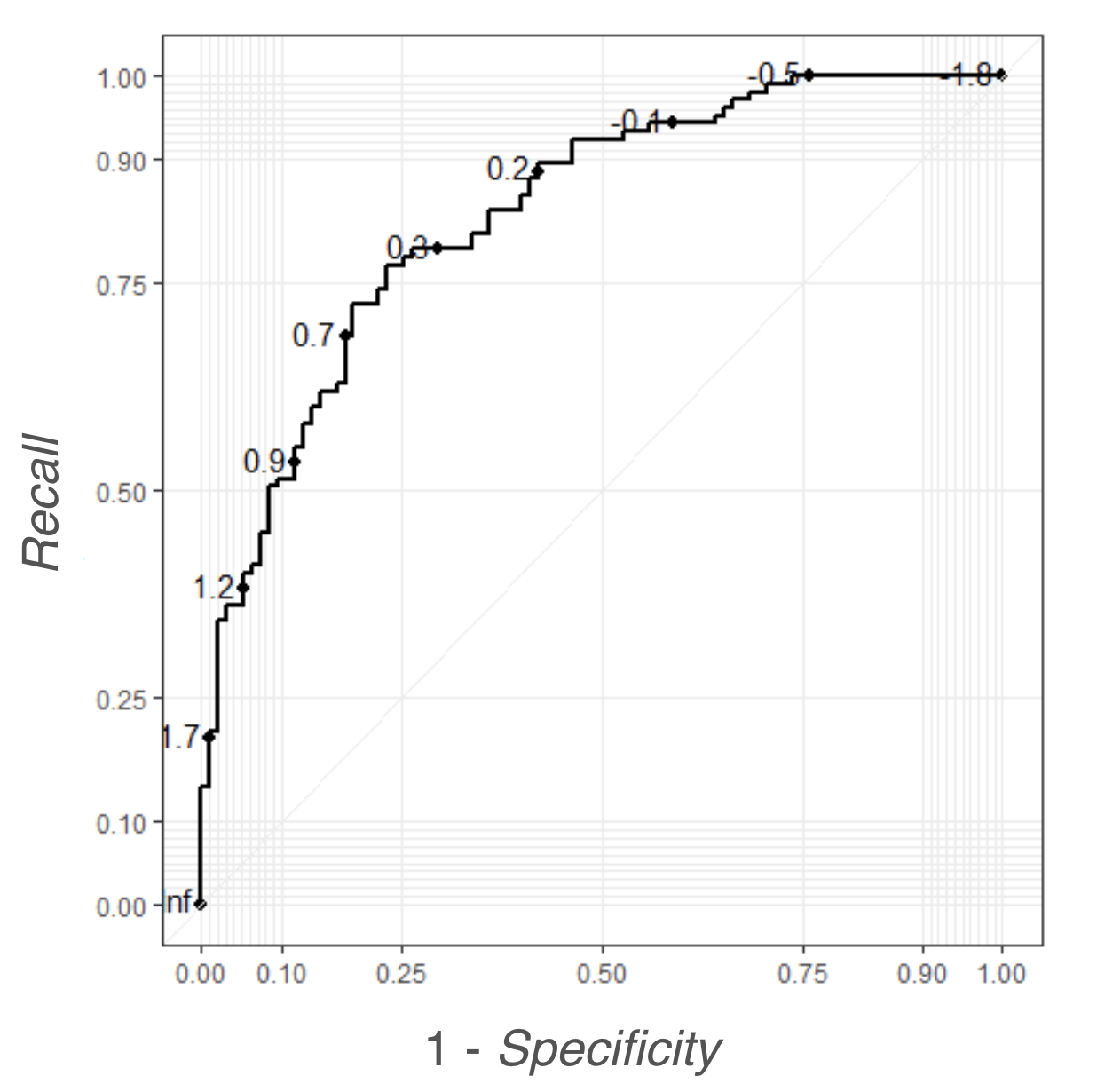
ROC 曲線越靠近左上角，代表分類模型的分類能力越好：給定 1 – Specificity 很靠近 0 （分類模型的門檻機率很靠近 0）卻能夠有很高的 Recall，代表分類模型預測出來的機率能夠很清楚的區分陰性跟陽性：預測陽性機率只要稍微大於 0 ，就很有可能是真正的陽性個體。因此，如果 ROC 曲線的曲線下面積 AUC 越靠近 1，就拜表分類模型的表現越好。值得一提的是，Recall 跟 Specificity 其實都不容易受到「不平衡資料」(TP + FN << TN + FP) 的影響：Recall 公式中的 TP, FN 都只跟陽性個體有關，而 Specificity 的 TN, FP 也只跟陰性個體有關，因此 ROC 曲線跟 AUC 在不平衡資料下仍然是適合的衡量指標。

常見的衡量指標：F-指標

另外一組常用的指標是 Precision 與 Recall。通常在做不平衡資料的分類模型時，模型很容易傾向說一個個體為陽性，但這並不一定是一件好事。以盜刷作為例子，假設我們找到了一個機器學習模型，預測 2% 的交易為盜刷，而且這些被預測為盜刷的交易，包含了所有真正盜刷的交易，以 Recall 的角度出發，這個模型非常好，但是會不會很容易打擾到那些不是盜刷的卡戶呢？這時我們就可以拿 Precision = 0.5% / 2% = 0.25，看起來不是很高。如果我們有另一個模型，預測 1% 的交易量為盜刷，而且有八成的盜刷交易被包含在模型預測為陽性的個體中，包含了所有 80% 的盜刷交易，這時雖然 Recall 變成了 0.8，但是 Precision = 0.4% / 1% = 0.4 卻提升了不少。

通常，我們會希望一個模型他的 Precision 與 Recall 都不要太差，因此我們常會使用 F-指標作為不平衡分類問題的衡量指標。F-指標是 Precision 跟 Recall 的調和平均數，也就是：

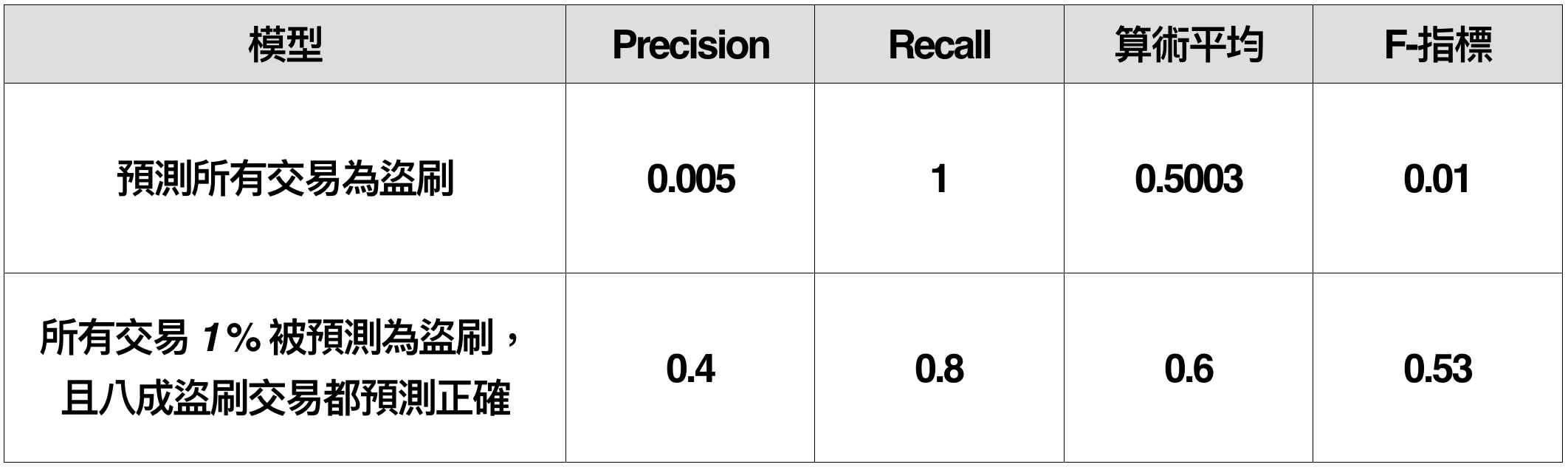
為什麼要用調和平均呢？假設盜刷分類問題中，我們有模型 1：所有的交易都當成盜刷，模型 2：預測 1% 的交易量為盜刷，而且有八成的盜刷交易被包含在模型預測為陽性的個體中。你會發現，模型 2 明明比 模型 1 好得非常多，但 Preccision 和 Recall 的算術平均卻沒有差太多，反之 F-指標區分模型好壞的能力強上許多。

如何建立一個好的不平衡分類模型？

討論完怎麼有效衡量不平衡二元分類模型的好壞，問題是不是就此迎刃而解了呢？其實不然，分類模型的訓練其實也是一個麻煩！在不平衡資料下進行分類，時常遇到陽性跟陰性各個維度特徵 (Feature) 的差異可能並不明顯。比如說：假設盜刷交易 (佔 0.5%) 的交易金額在 8000 – 12000 元，非盜刷交易 (佔 99.5%) 的金額可能落在 100 – 13000元，而非盜刷交易在 8000 – 12000 的金額可能佔總交易 35%。此時，如果有一筆交易是 10000 元，直接猜測這筆交易不是盜刷猜對的機率是  98.6%，還是非常高！在這樣的情況下，機器學習的算法其實很難區分出到底一筆交易是不是陽性的。

如果遇到上面這樣的問題，可能最直接會想到的解決方法就是「蒐集新的特徵」，找到一個很容易區分出陽性與陰性的特徵不就好了嘛！但是事情並沒有這麼簡單，要是有這麼好的特徵，根本就不需要做機器學習啊！所以，在不能蒐集更多新特徵的條件下，我們其實有以下幾種常見的處理方法：

• 抽樣方法：
  透過個體的複製與刪除，創造出比較平衡的資料集合，比如說：
  • Oversampling：隨機複製陽性個體，使陽性與陰性在訓練集合的比例達到 1:1，這種方法最大的缺點是很容易讓 Specificity 下降。
  • Undersampling：隨機刪除陰性個體，使陽性與陰性在訓練集合的比例達到 1:1，這種方法最大的缺點是很容易缺失某些陰性個體的資訊。

• 產生合成樣本 (Synthetic Sample)：
  根據原本陽性樣本的分佈特徵，模擬出很類似的新陽性樣本，比如說：
  • SMOTE / AdaSyn 等利用「最近鄰點」(Nearest Neighbors) 為出發的方法產生新資料
  • 利用貝氏網絡 (Bayesian Network) 產生具有相似變數結構的新資料
  • GAN：利用生成與對抗模型產生相似分配的資料 (可以參考很潮的網站：https://poloclub.github.io/ganlab/)

• 成本導向的機器學習模型 (Cost-sensitive Classification)：將一般機器學習的損失函數 (loss function) 改為成本導向的損失函數。

在這個系列的下一篇文章中，我們會仔細介紹有哪些常見的 抽樣 / 產生合成樣本 的方法，幫助我們做不平衡資料的二元分類問題。有關 David’s Perspective 的最新文章，都會發布在大鼻的 Facebook 粉絲專頁，如果你喜歡大鼻的文章，還請您按讚或留言給我喔！

大鼻觀點：https://www.facebook.com/davidperspective/