利用「個體經濟模型」設計與評估新聞推薦系統

今天想跟大家介紹一篇對做推薦系統很有啟發的論文：When and How to Diversify—A Multicategory Utility Model for Personalized Content Recommendation，利用個體經濟學中「消費者決策」理論，建立更符合消費者決策邏輯的推薦模型。這類模型特殊的地方有二，一是試圖建構消費者在瀏覽文章時的「決策過程」—也就是最大化效用 (Utility Maximization) 的過程，並考量多種不同的選擇行為。二是可以透過消費者過去已經觀看文章的類型，考量同一 session 中不同步驟時文章類別互相替代與互補的關係。我自己非常喜歡這個方向的推薦系統研究，有時候一味追求更複雜的演算法，可能效果不一定會比更貼近真實決策過程的演算法來的好，因此跟大家分享這篇論文。

單一 session 內的使用者決策過程

在一個 session 內，使用者在挑選「新聞文章類別」時有幾個重要的行為。首先，在挑選類別時使用者會試圖極大化自己在這次 session 結束前的期望效用，也就是看這些文章帶來的滿足感，而不同類別的文章可能會有替代效果 (substitution effect)，比如說：娛樂新聞跟社會新聞可能只會想選一個類別看，也有可能會有互補效果，比如說：看完經濟類文章可能會想繼續閱讀政治類新聞。

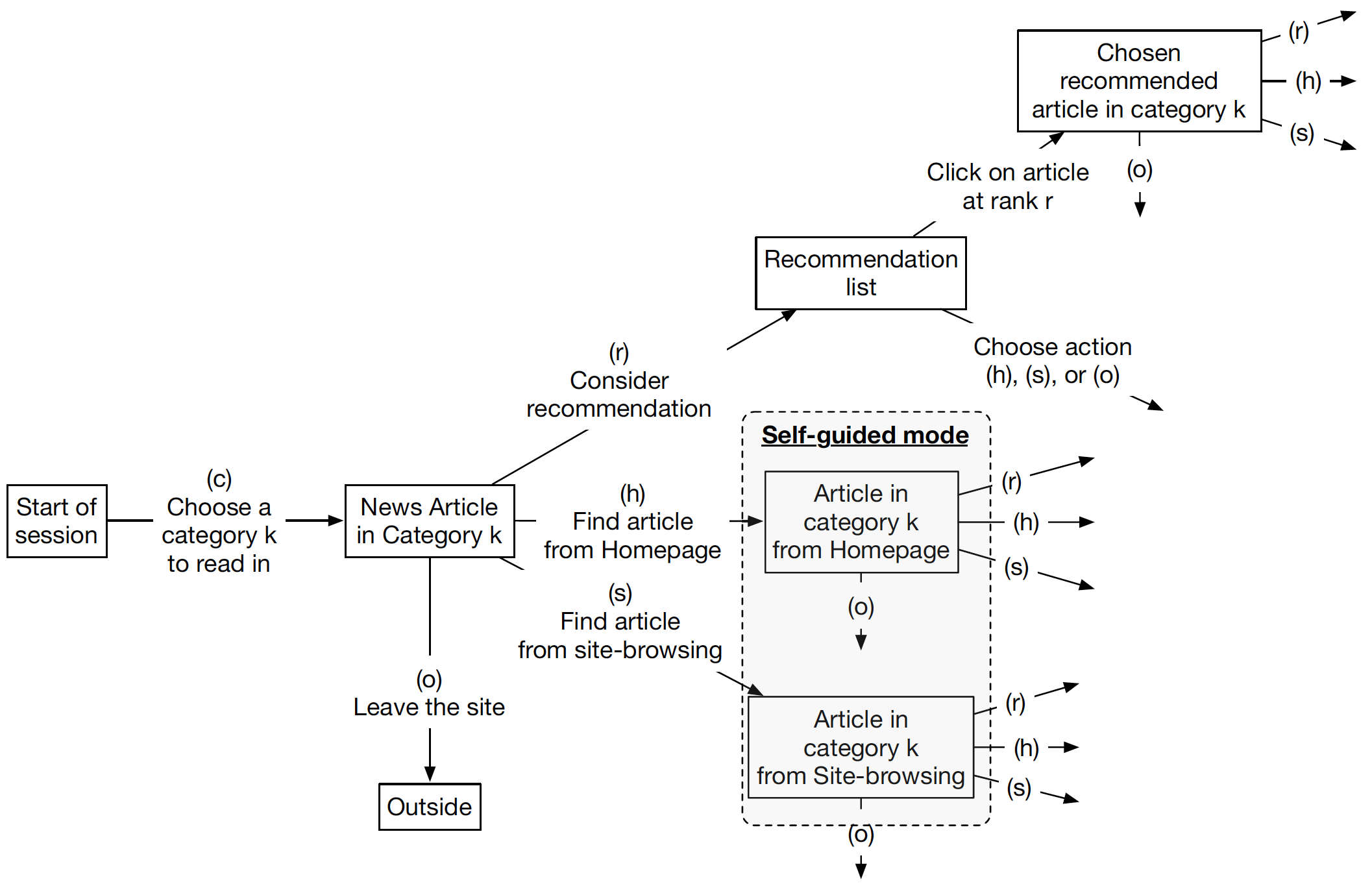
此外，使用者可能會選擇從「推薦系統」挑選文章類別，也有可能自己從首頁或其他地方找到文章，但靠使用者自己找到的文章會有較高的搜尋成本，此為使用者也會考量對於「推薦系統」跟「自行搜尋」所得到文章的信心。最後，當使用者自己無法從繼續閱讀文章得到正的效用時，他們會選擇停止閱讀。根據上面的行為模式，我們可以將整個使用者決策過程總結成下圖的決策樹。

使用者的滿足感：CES 效用函數

首先，我們假設使用者在不同 sessions 觀看文章的行為只受到個人對於不同內容的基本偏好影響，不會有其他跨 session 因素影響使用者行為。接著，我們假設使用者在不同文章類別的替代效果彈性為一個固定的常數，也就是所謂的 CES (Constant Elasticity of Substitution) 模型。令 $latex x_{ku}^t$ 為在 session 中累積到第 $latex t$ 篇文章時類別 $latex k$ 文章被使用者 $latex u$ 觀看的篇數； $latex a_{ku}$ 是使用者 $latex u$ 對於類別 $latex k$ 的喜好分數；$latex s_u$ 是使用者對於不同類別的替代效果，如果 $latex s_u \rightarrow 0$ 代表使用者把不同類別的文章當作完全互補品，而 $latex s_u \rightarrow \infty$ 代表使用者把不同類別的文章當作完全替代品。此時的效用函數模型如下：

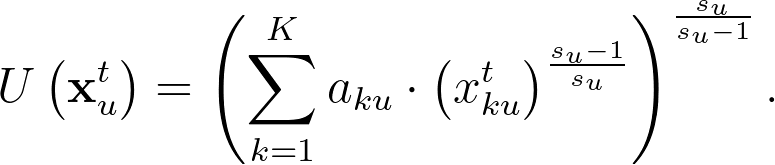
此處假設使用者的偏好係數符合多元對數常態分配， $latex \log(\mathbf{a}_u) \sim \mathcal{N}(\boldsymbol\mu_a,\Sigma_a)$，其中 $latex \boldsymbol\mu_a$ 代表著所有讀者的基本偏好，$latex \Sigma_a$ 代表著不同類型文章彼此間的相關性。另外假設替代彈性 $latex \log(s_u) \sim \mathcal{N}(\theta_s, \sigma_s)$。

上處的方程式刻畫了使用者在一個 session 結束時或得到的期望效用。接著，我們要估計「使用者 $latex u$ 如果額外多看了一篇類別 $latex k$ 的文章，會增加多少的邊際效用 (marginal utility)？」對 $latex x_{ku}^t$ 微分，我們可以得到「新看一篇類別 $latex k$ 文章」額外增加或減少的邊際效用：

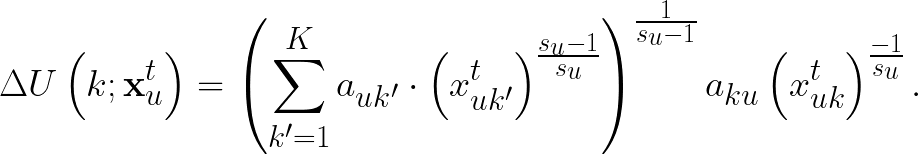
此處，我們也要進一步考量消費者轉換類別時，可能會需要重新習慣新的主題，因而感到麻煩使效用下降。此處的「轉換成本」(switching cost) 是透過所有使用者整體的「轉換機率」來估計：令 $latex T(k’, k)$ 為使用者從文章類別  $latex k’$ 轉換到文章類別 $latex k$ 的機率，則轉換成本應該會正比於 $latex D(k’,k) = 1 – T(k’,k)$ （越不可能轉換的兩個文章類別，其轉換成本應該越高）。此外，每位使用者對於轉換的偏好也有可能不一樣，因此令 $latex C_u^{switch}$ 為使用者 $latex u$ 的轉換成本，並假設 $latex \log(C_u^{switch}) \sim \mathcal{N}(\theta_{switch}, \sigma_{switch})$。因此，我們在原本的邊際效用公式上加入額外的「轉換成本」$latex C_u^{switch}D(k’,k)$，因此「使用者從 $latex k’$ 類別轉換到 $latex k$ 類別多看一篇文章」的邊際效用最後為：

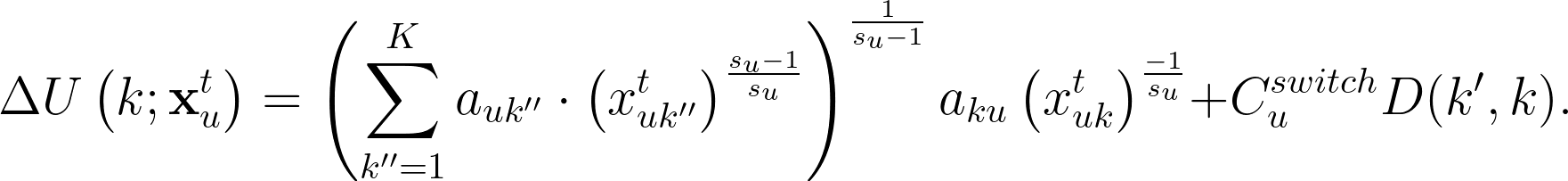
使用者對不同文章來源的品質認知

接下來，我們針對使用者對於推薦 (recommendation)、首頁 (homepage) 與瀏覽 (site-browsing) 等不同文章來源得到文章品質的認知進行建模。首先，假設使用者在初步瀏覽過網頁文章的簡介後，認為品質良好的因此可以透過文章的「點擊率」（假設服從 Beta 分配）來衡量品質。令使用者 $latex u$ 到 $latex \tau$ 時間點（包含所有 session 的資訊）對於「推薦系統」文章的瀏覽次數為$latex n_{ru}^{\tau}$、點擊次數為 $latex n_{rug}^{\tau}$，則我們可以得到推薦系統點擊率的後驗分配 (posterior distribution) 為 $latex p_{ru}^tau \sim Beta(\alpha_{ru}^\tau , \beta_{ru}^tau )$，其中

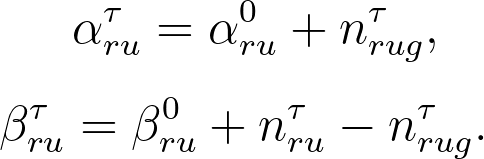
因此，使用者對於「推薦系統」文章點擊率的 posterior mean 為 $latex \overline{p_{ru}^{\tau}} = \frac{\alpha_{ru}^{\tau}}{\alpha_{ru}^{\tau}+\beta_{ru}^{\tau}}$。同時，我們也可以得到「如果使用者 $latex u$ 從 $latex k’$ 類別轉換到推薦系統推薦 $latex k$ 類別的一篇文章」，使用者的期望效用變化就是：

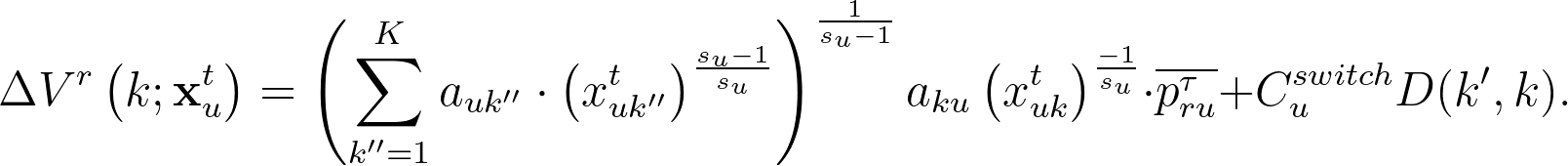
同樣的道理，我們也可以建立從首頁或瀏覽來的期望效用 $latex \Delta V^h\left(k; \mathbf{x}^t_u \right ), \Delta V^s\left(k; \mathbf{x}^t_u \right ) $。論文中假設消費者對於首頁、瀏覽等其他渠道的文章品質認知不會改變，也就是 $latex \overline{p_{hu}^{\tau}, \overline{p_{su}^{\tau}$ 一直不會隨著點擊紀錄的累積而更新。

瀏覽推薦系統的點擊機率

點擊與否除了使用者對於文章品質的主觀認知外，還有一個可能因為文章出現的位置以及其他沒有被考慮到效用模型裡這的因素。為了考慮沒有被效用模型捕捉到的資訊，可以利用 $latex \epsilon$ 這個常數值控制 —— 當 $latex \Delta V^r\left(k; \mathbf{x}^t_u \right ) + \epsilon >=0$ 時使用者才會點擊該文章。另外，論文中利用邏輯迴歸模型來分析使用者會不會點擊第 $latex i$ 個位置的文章（令該文章的文章類別為 $latex k$），也就是：

因此，使用者在推薦文章清單中，點擊第 $latex n$ 個位置文章的機率就可以寫成：

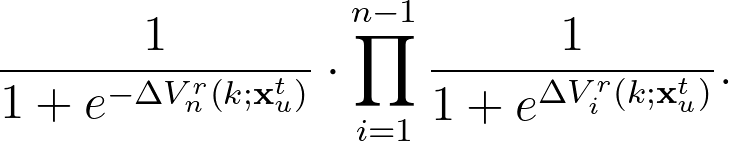
文章來源的選擇

最後，我們可以透過每個文章來源的估計出的邊際效用，建立多元邏輯迴歸模型。首先，在新聞推薦網站中有四個主要的來源選擇：瀏覽推薦系統、瀏覽首頁、自行在網站上搜尋、以及直接離開網站。令推薦系統推薦使用者 $latex u$ 文章類別 $latex K$ 的機率為 $latex P_{u}^r(k)$，則使用者是否選擇「推薦系統」的文章會受到推薦系統帶來的期望效用 $latex \sum_{k=1}^K P_{u}^r(k) \cdot \Delta V^r\left(k; \mathbf{x}^t_u \right ) $ 影響。假設推薦系統總共推薦了 $latex r$ 篇文章，考量不點擊的機率（$latex 1- \mathbb{P}(No~Click)$）與推薦系統的搜尋成本（瀏覽、滑動等）$latex C^r_u$（服從對數常態分配），則「推薦系統的總效用」為：

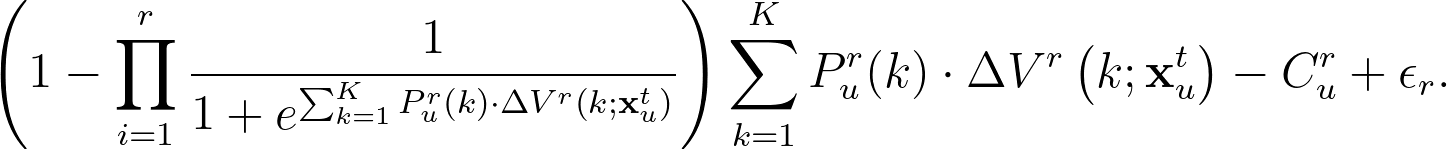
同理，我們也可以得到選擇「網站首頁」與「自行瀏覽」文章後獲得的邊際效用（如果是直接離開，邊際效用則為 $latex 0$）：

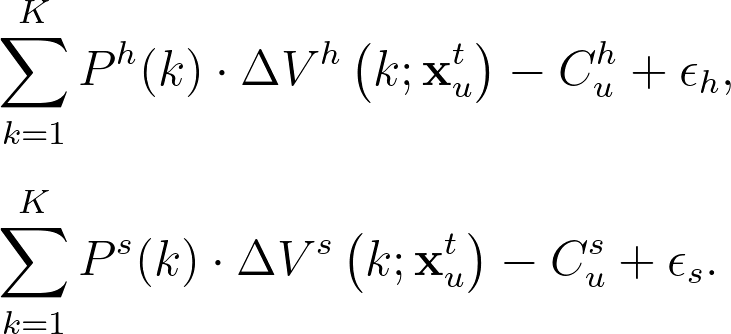
整合使用者決策過程的推薦系統

接下來，根據上面的討論，我們可以將使用者的決策過程串接成一個決策與推薦系統，並根據使用者的瀏覽點擊紀錄了解使用者對於不同新聞類別的偏好與不同文章來源品質的認知。整個過程步驟如下：

1. 從 $latex K$ 個文章類型中選擇一種文章類型 $latex k$，此時邊際效用增加為 $latex \Delta U(k;\mathbf{0})=a_{ku}^{\frac{s_u}{s_u-1}}$
2. 根據四個不同文章來源（推薦、首頁、自行瀏覽、離開網頁）帶來的邊際效用與多元 logit 模型選擇其中一個文章來源，其中邊際效用計算的公式為：
   
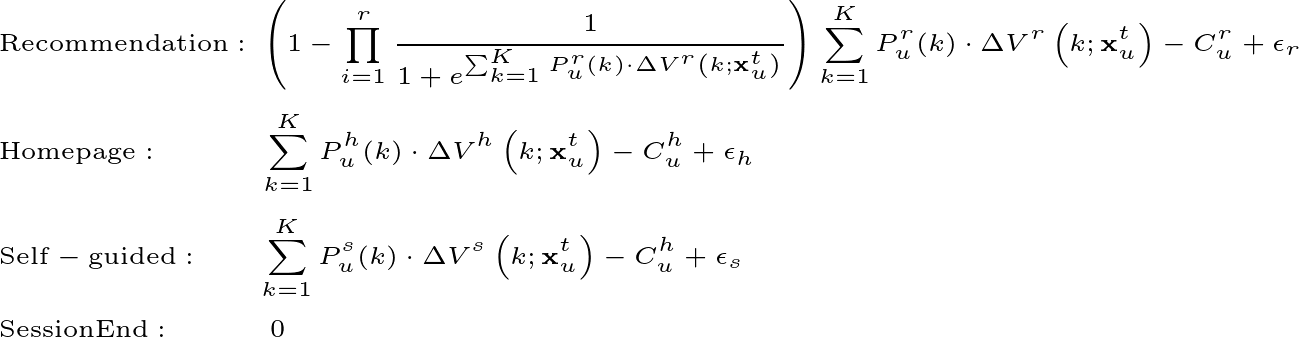
3. 如果使用者選擇瀏覽推薦清單，則根據以下機率模式點擊第 $latex n$ 個位置的文章
   
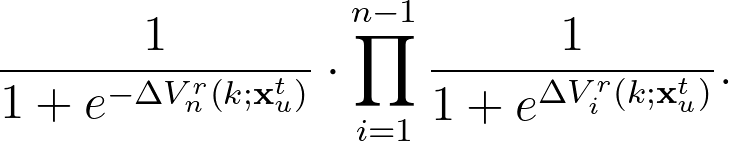
   如果使用者沒有點擊任何文章，會回到 2. 選擇首頁、自行瀏覽或離開網頁。
4. 如果使用者選擇首頁、自行瀏覽，則根據以下公式選擇文章類別閱讀：
   
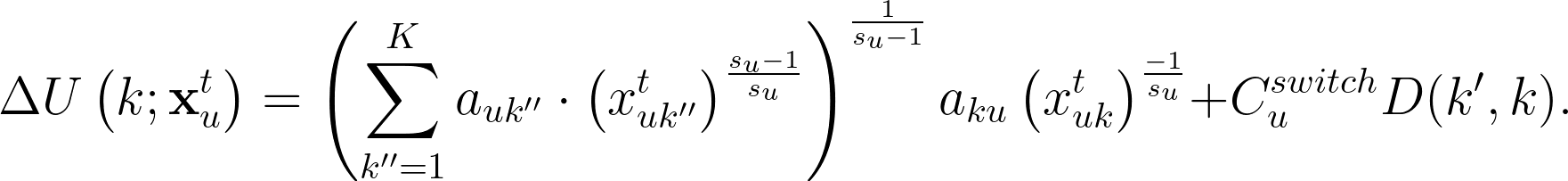
5. 如果選擇離開網頁，則 session 結束。

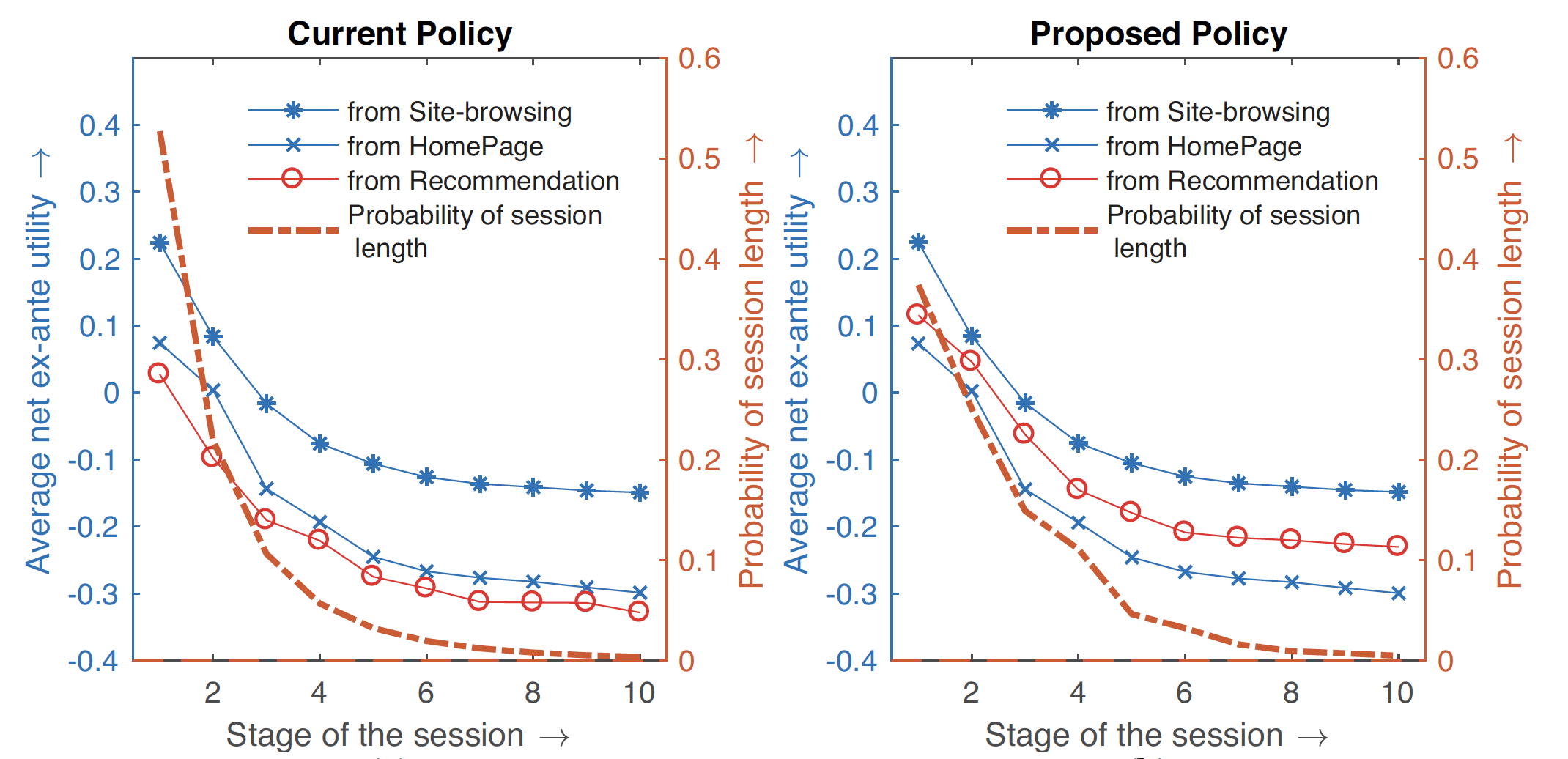
上面的參數估計過程可以利用 MCMC (Markov Chain Monte Carlo) 方法進行估計。此外，這篇論文也透過上面得到對於不同類別的偏好，提出了 MCUwCES 的推薦演算法，下圖則是分析了原始演算法跟 MCUwCES 演算法對於使用者在同一 session 隨著點擊增加邊際效用的影響，有興趣可以更仔細的閱讀這篇論文的原文。

有關 David’s Perspective 的最新文章，都會發布在大鼻的 Facebook 粉絲專頁，如果你喜歡大鼻的文章，還請您按讚或留言給我喔！

大鼻觀點：https://www.facebook.com/davidperspective/