生成模型與文字探勘：利用 LDA 建立文件主題模型

在「機器學習中的貝氏定理：生成模型與判別模型」文章中有提到，生成模型主要的精神是「學習資料的生成機制」，因此在生成模型中，我們會觀察大量資料，估計出資料的生成機制，並用單純貝氏分類器 (Naive Bayes Classifier) 作為例子，解釋了生成模型的原理。在今天的文章中，我們要跟大家介紹一個自然語言處理中非常有名的方法−隱含 Dirichlet 配置模型 (Latent Dirichlet Allocation，簡稱 LDA)，透過生成模型的機制，在一系列文件中萃取出抽象的「主題」。

LDA 的基本精神：文件生成的機制

假設我們蒐集到了一組文本 (Corpus) $latex \mathcal{D} = \begin{Bmatrix} \mathbf{w}_1, & \mathbf{w}_2, & \cdots, & \mathbf{w}_M \end{Bmatrix}$，其中 $latex \mathbf{w}_{i} = \begin{bmatrix} w_{i1}, & w_{i2}, & \cdots, & w_{iN_i}  \end{bmatrix}$ 代表第 $latex i $ 個文件，$latex w_{ij}$ 代表第 $latex i $ 個文件的第 $latex j$ 個用詞，總共用了 $latex V$ 個用詞的詞庫來撰寫這些文件。

LDA 有趣的地方是，該模型假設了「人類撰寫一篇有意義文件」的隱含機制：每篇文件都是由少數幾個「主題 (Topic)」所組成，而且每個主題都可以由少數幾個重要的「用詞 (Word)」描述。在 LDA 模型中，我們假設文本 $latex \mathcal{D}$ 生成時，背後有 $latex K$ 個重要的隱含主題 。每個主題 $latex t = 1, 2, \cdots, K$ 都可以用 $latex V$ 個用詞中的其中幾個用詞來描述。文件中的每個用詞 $latex w_{ij}$ 其實都對應到這 $latex K$ 個主題中的一個主題，我們將這個用詞的主題紀錄為 $latex T_{ij}$。下面的圖示清楚解釋 LDA 在描述「主題−用詞−文件」間的關聯，然而在真實的世界中，我們唯一觀察到的就是文本，因此主題與對應的用詞是我們需要透過觀察大量文本來推論出的結構。

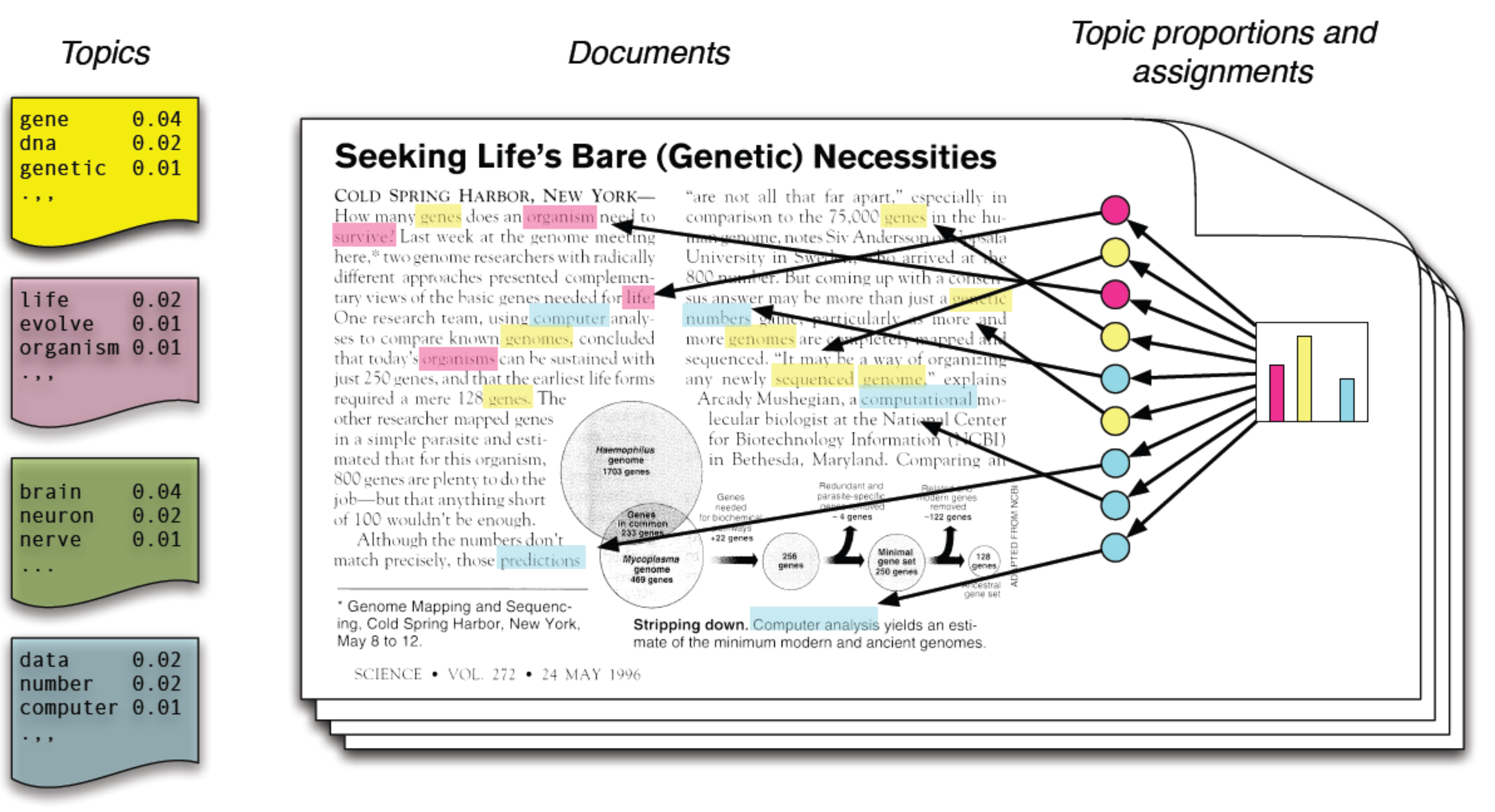
總結來說，LDA 假設人們在撰寫該文本的一篇文件時，有以下幾個重要的生成步驟：

• 決定第 $latex i $ 篇文件的用詞數 $latex N_i$

• 決定第 $latex i $ 篇文件在 $latex k$個主題各自出現的傾向程度為 $latex \boldsymbol\theta_i = \begin{bmatrix} \theta_{1}, & \cdots, & \theta_{k}\end{bmatrix}$。

• 撰寫第 $latex i $ 篇文件的第 $latex j$ 個用詞 $latex w_{ij}$時：
  (1) 會先選擇一個對應的主題 $latex z_{ij} = t$；
  (2) 根據主題 $latex t$，接著挑選一個可以用來描述該主題的用詞當作 $latex w_{ij}$；
  (3) 對於第 $latex t$ 個主題，詞庫中用詞各自出現的傾向程度為 $latex \boldsymbol\phi_t = \begin{bmatrix} \phi^t_{1}, & \cdots, & \phi^t_{V}\end{bmatrix}$。

LDA 模型的先驗機率分配

有了上述的「文件生成機制」後，我們接著就會透過觀察大量文件資料，估計文件生成的聯合機率分配。在 LDA 中，我們使用以下的先驗分配 (Prior Distribution) 來描繪上述的文件生成機制（以貝氏網絡圖表示，其中圓圈底色為灰色代表「可觀察到的資料」，圓圈底色為白色則代表「隱含配置」(Latent Allocation)）：

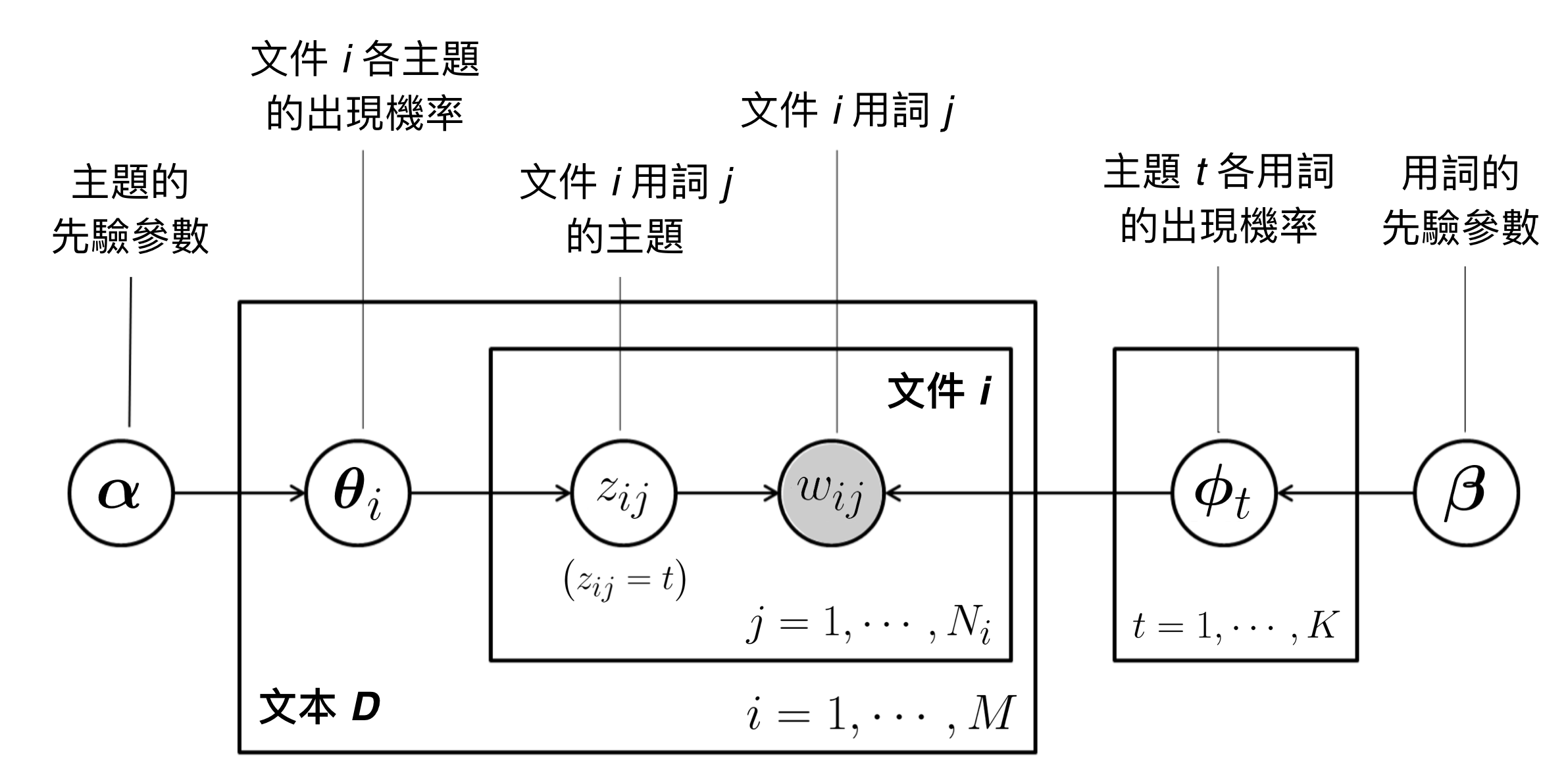
• 一篇文件的用詞數 $latex N_i \sim \textrm{Poisson} (\xi)$：
  在機率理論中，卜瓦松分配 (Poisson Distribution) 是用來描繪「計數資料」(Count Data)，比如說：一家店一天的來客數。在此處，我們用 Poisson 分配來描述「一篇文本的用詞數」，其中 $latex \xi$ 代表該文本中各文件的平均用詞數。

• 第 $latex i $ 篇文件的第 $latex j$ 個用詞時在各個主題出現的次數 $latex z_{ij}\sim \textrm{Multinomial} (1, \boldsymbol\theta_i)$ ：
  在機率理論中，多項分配 (Multinomial Distribution) 代表的是：假設有 $latex 1$ 次實驗（撰寫 $latex 1$ 個用詞），該次實驗出現結果是主題 $latex t$ 的機率為 $latex \theta_t$。

• 第 $latex i $ 篇文件 $latex k $ 個主題各自的出現機率 $latex \boldsymbol\theta_i \sim \textrm{Dirichlet}(\boldsymbol\alpha)$：
  此處選擇 Dirichlet 分配作為先驗分配，主要是因為多項分配參數的共軛分配 (Conjugate Prior) 是 Dirichlet 分配。也就是說，$latex \boldsymbol\theta_i$ 根據資料更新後，其後驗分配 (Posterior Distribution) 仍然是Dirichlet 分配。

• 給定主題 $latex z_{ij} = t$，第 $latex i $ 篇文件的第 $latex j$ 個用詞在詞庫中各個用詞各自出現的機率 $latex w_{ij} \sim \textrm{Multinomial} (1, \boldsymbol \phi_t  )$：同理，多項分配描述的是：撰寫 $latex 1$ 個用詞時，結果是用詞 $latex v$ 的機率為 $latex \phi^t_v$。

• 第 $latex t$ 個主題每個用詞的出現機率 $latex \boldsymbol\phi_t  \sim Dirichlet(\boldsymbol\beta)$：
  LDA 除了假設每篇文章各主題出現的次數為多項分配外，也假設「每個主題各個用詞出現的次數」為多項分配，因此

LDA 模型的推論問題

定義完 LDA 模型的架構後，我們可以得到資料生成的機制，也就是參數與資料的聯合機率分佈 (joint probability distribution)：，

其中 $latex \mathbf{z} = \begin{Bmatrix} \mathbf{z}_1, & \mathbf{w}_2, & \cdots, & \mathbf{z}_M \end{Bmatrix},~\mathbf{z}_i = \left[z_{i1}, \cdots, z_{iN_i}\right]$ 代表各個文件的每個用詞對應到的主題。然而，上述的聯合機率分佈並不是最終的目標，我們真正希望能學習到的是基於「觀察文本 $latex \mathcal{D}$ 中大量文件」所得到各個文件的「主題」分佈與各個主題的「用詞」分佈，也就是得到$latex \boldsymbol\theta,\mathbf{z},\boldsymbol\phi$ 的後驗分佈 (Posterior Distribution) ：

，

這個步驟在貝氏統計中稱為「推論」(Inference)。然而，推論最大的難題就在於：實際上在一個文件 $latex \mathbf{w}_i \in \mathcal{D}$被撰寫時，他的主題 $latex \mathbf{z}_i$ 與主題相關選用詞  $latex \boldsymbol\phi_{\mathbf{z}_i}$  都是預先決定的，我們並不知道如果沒有給定 $latex \mathbf{z}_i$ 與 $latex \boldsymbol\phi_{\mathbf{z}_i}$，該文件的生成機制 $latex \mathbb{P}\left(\mathcal{D}|\boldsymbol\alpha,\boldsymbol\beta,\xi\right)$ 是什麼。因此，在原始 LDA 的論文中採用的是很常見的貝式估計方法 − Variational Inference。在這裡我們要跟大家介紹一個效能更好的方法，稱作 Collapsed Gibbs Sampling。

Gibbs Sampling 基本概念

Gibbs Sampling 的概念很簡單，假設有一未知的聯合機率分配 $latex \mathbb{P}(\mathbf{z}_1,\cdots, \mathbf{z}_m)$，但我們知道給定其他變數下，$latex   \mathbf{z}_i$ 的條件分配 (Conditional Distribution) $latex \mathbb{P}(\mathbf{z}_i| \mathbf{z}_1, \cdots, \mathbf{z}_{i-1},\cdots, \mathbf{z}_{i+1} \mathbf{z}_m)$，則我們可以透過以下的馬可夫鏈蒙地卡羅 (Markov Chain Monte Carlo) 過程，再經過 $latex T$ 的模擬後得到近似 $latex \mathbb{P}(\mathbf{z}_1,\cdots, \mathbf{z}_m)$ 的分配，其中的估計方法如下：

• 從 $latex \widetilde{\mathbf{z}} = (\mathbf{z}_1,\cdots, \mathbf{z}_m)$ 的先驗分配中抽出一組樣本 。

• 對於 $latex t= 1, 2, \cdots, T$，我們要從 $latex \mathbb{P}(\widetilde{\mathbf{z}}^{(t)})$ 中抽樣出 ：
  • 從 $latex \mathbb{P}(\mathbf{z}_1 | \mathbf{z}^{(t)}_2, \cdots, \mathbf{z}^{(t)}_m)$ 中抽出一個隨機樣本 $latex \mathbf{z}^{(t+1)}_1$
  • 從 $latex \mathbb{P}(\mathbf{z}_2 | \mathbf{z}^{(t+1)}_1, \mathbf{z}^{(t)}_3, \cdots, \mathbf{z}^{(t)}_m)$ 中抽出一個隨機樣本$latex  \mathbf{z}^{(t+1)}_2$
  • …
  • 從 $latex \mathbb{P}(\mathbf{z}_m | \mathbf{z}^{(t+1)}_1, \mathbf{z}^{(t+1)}_2, \cdots, \mathbf{z}^{(t+1)}_{m-1})$ 中抽出一個隨機樣本$latex  \mathbf{z}^{(t+1)}_m$

透過重複隨機抽樣逐漸逼近真實分配的概念叫做「蒙地卡羅模擬」(Monte Carlo Simulation)，而 Gibbs Sampling 最大的好處是：儘管前面抽樣出了 $latex  \widetilde{\mathbf{z}}^{(1)}, \cdots, \widetilde{\mathbf{z}}^{(t)}$ 這麼多組的樣本，但 $latex \widetilde{\mathbf{z}}^{(t+1)}$ 的條件分配只跟 $latex   \widetilde{\mathbf{z}}^{(t)}$ 有關，這樣的性質叫做馬可夫性質。Gibbs Sampling 其實是具有定態分配 (stable distribution) 的馬可夫鏈 (有限遍歷性馬可夫鏈)，也就是指：存在一個分配使得  $latex \mathbb{P}(\widetilde{\mathbf{z}}^{(t+1)}) = \int \mathbb{P}(\widetilde{\mathbf{z}}^{(t)}) d \mathbb{P}(\widetilde{\mathbf{z}}^{(t+1)}|\widetilde{\mathbf{z}}^{(t)})$，也就是說：當你模擬了足夠多次後，在這之後你抽出的這些樣本的形成的分配會跟 $latex \mathbb{P}(\mathbf{z}_1,\cdots, \mathbf{z}_m)$ 一致。

LDA 與 Collapsed Gibbs Sampling 

接下來，我們可以仔細跟大家介紹 LDA 是怎麼樣學習「主題」的。儘管 LDA 有幾個隱藏的參數需要估計後驗分配，包括：$latex \boldsymbol\theta,\mathbf{z},\boldsymbol\phi$，但實際上只要得到每個文件每個用字的主題 $latex \mathbf{z}$ 的分配， $latex \boldsymbol\theta,\boldsymbol\phi$ 的分配自然就可以估計出來的。因此我們在進行 Gibbs Sampling 的時候，只需要針對 $latex \mathbf{z}$ 進行抽樣即可。這種省略其他隱含變數的方法，就叫做 Collapsed Gibbs Sampling。

為了簡化符號，令 $latex \mathbf{z}_{-i} = \mathbf{z}_1, \cdots, \mathbf{z}_{i-1},\cdots, \mathbf{z}_{i+1} \mathbf{z}_m)$。若要得到 Gibbs Sampling 用來抽樣的分配，我們需要試著得出 $latex \mathbb{P}\left(\mathbf{z}_i|\mathbf{z}^{-i},\mathcal{D}\right)$ ，也就是要把其他的參數都想辦法處理掉，單純以觀察到的文本 $latex \mathcal{D}$ 與先前已經抽樣出的 $latex \mathbf{z}^{-I}$ 表達分配。因此，我們從已經知道的分配出發：給定其他文件的主題，第 $latex i$ 個文件主題的機率分配為：

，

其中由於分母與此處唯一的變數 $latex \mathbf{z}_{i}$ 無關，因此可以視為常數省略，另外由於文本中每篇文章的字數已經知道，因此我們已經可以估計出 $latex \xi$ ，在下面的推導中不在討論。接下來，我們可以將上式與我們先前已經知道的生成機制−參數與資料的聯合機率分佈進行連結：

，

接下來，我們可以根據積分的左右兩部分別求解：左側我們知道 $latex \mathbb{P}\left(\boldsymbol\theta|\boldsymbol\alpha\right)$ 是 $latex M$ 個  $latex  \textrm{Dirichlet}(\boldsymbol\alpha)$ 分配相乘，$latex \mathbb{P}\left(\mathbf{z}|\boldsymbol\theta\right)$ 是 $latex M \times \sum_{i = 1}^{M} N_{i}$ 個  $latex \textrm{Multinomial} (1, \boldsymbol\theta_i)$分配相乘，相乘在一起可以透過 Dirichlet 分配的積分技巧得到解析解：

，

其中 $latex n_{ik}$ 代表第 $latex i$ 篇文件中屬於主題 $latex k$的用詞數，$latex B(\boldsymbol\alpha) = \frac{\prod_i \Gamma(\alpha_i)}{\Gamma(\sum_i \alpha_i)}$ 為多項 Beta 函數。同理，我們也可以用相同的觀念與技巧得到右側的積分式：

。

將左右兩側積分結果合併，我們可以得到以下結果，其中 $latex \mathbf{n}_i = \left[n_{i1},\cdots,n_{iK}\right]$

。

令$latex \mathbf{n}^{(-i)}_{a} = \left[n_{a1}, \cdots, n_{a(i-1)},  0, n_{a(i+1)}, \cdots, n_{ak}\right]$，我們可以用上述的公式得到 Gibbs Sampling 中更新參數分配重要的步驟（在此省略 Beta 函數的運算細節）：

。

總結：LDA 與 Gibbs Sampling 的算法

基於上述的推導，我們可以得到 Gibbs Sampling 的算法如下：

LDA 數學雖然複雜，但實作上其實非常簡單。此外，LDA 很容易被推廣，比如說：如果兩個文章的主題相關，我們可以利用 Logistic-Normal 模型建立 Correlated LDA；如果文章的順序重要（比如說：就職典禮演說隨時間的變化），我們可以透過 Logistic-Normal 模型建立主題隨時間改變的模式。因此，LDA 可以說是眾多主題模型的基石！

有關 David’s Perspective 的最新文章，都會發布在大鼻的 Facebook 粉絲專頁，如果你喜歡大鼻的文章，還請您按讚或留言給我喔！

大鼻觀點：https://www.facebook.com/davidperspective/