社會學家或是 C-level 管理階層通常特別想了解一項「政策」(policy) 或「事件」(event) 發生後對於一群特定個體的影響,比如說:東西德合併之後,對東德與西德的經濟發展有什麼影響?公司調整了員工的獎勵發放機制,對於員工的績效或是離職率有什麼衝擊?為了瞭解政策或事件對於個體的影響,通常我們會進行「比較研究」(comparitive study) − 比較受影響個體與未受影響個體在不同指標上的差異。
一個有效的比較研究,最重要的事情就是確保「受影響個體」真的可以與「未受影響的個體」比較,過去我們最常使用的方法是「隨機控制實驗」(randomized control experiment),將高度相似的個體分為「實驗組」與「對照組」,實驗組會受到政策或事件的影響,對照組則在實驗前後則沒有任何差異。然而,隨機控制實驗其實是理想假設下的做法,並未考量太多實際限制。比如說:如何確保實驗組跟對照組真的是相似的(永遠有做不完的 sanity check)?如何找到足夠多高度相似的個體做對照組(東西德顯然是沒有對照組)?當操作上有一定的困難度,沒有辦法做個體層級的測試(只能以地理區域區分實驗組與對照組而並非門市層級),該怎麼分析?
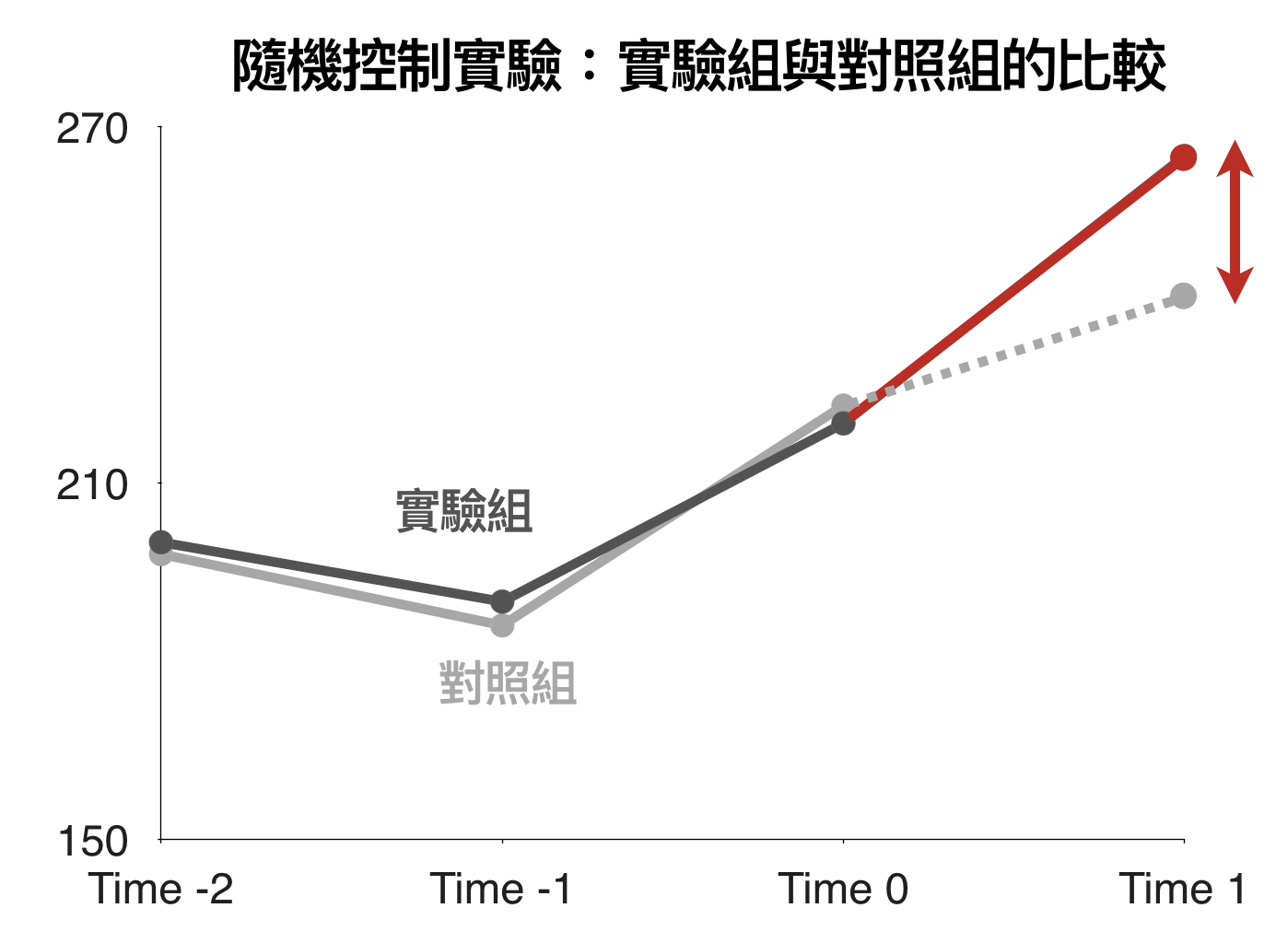
因果推論的三種工具:DID、時間序列、合成對照組
在社會科學中,儘管實施了隨機控制實驗,我們還是時常會遇到實驗組與對照組在衡量指標上有「尺度不匹配」的問題。比如說,儘管挑選了兩組銷售成長相近的門市,一組為實驗組,一組為對照組,但在測試前兩組門市的銷售金額就存在不小的落差。遇到這類問題時,我們時常採用 Difference-in-difference (DID) 方法進行分析,概念如下圖所示。
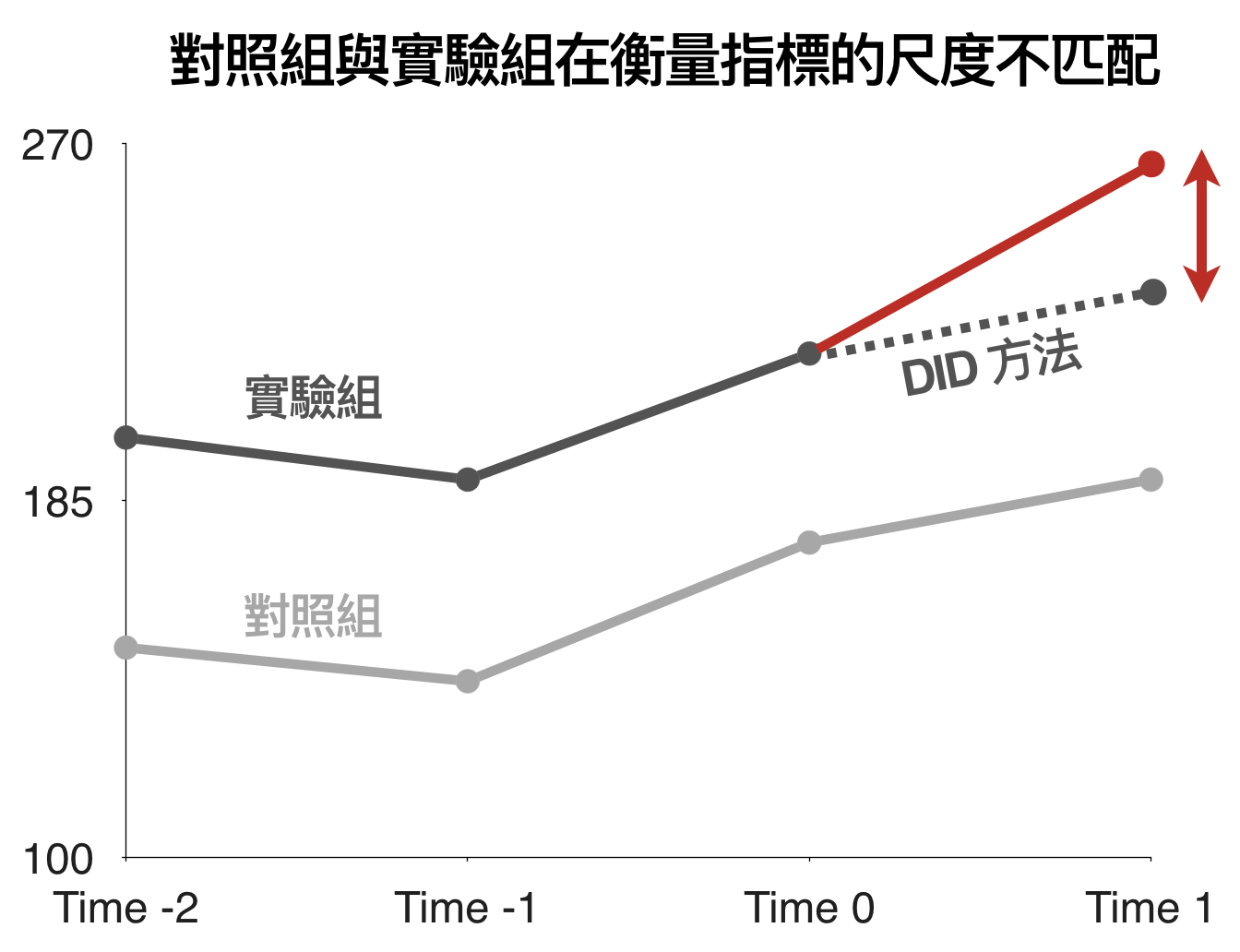
如果遇到「無法有任何對照組個體」的情況,這時有兩種類型的做法。第一種是「時間序列」的做法(概念如下右圖所示),比如說:我們想了解新推薦系統對於「商品點擊率」的影響,這時就可以基於過去的點擊率模型,預測未來的期望點擊率,並計算新系統上線後真實點擊率與期望點擊率的差異;時間序列預測最大的問題在於需要建立足夠準確的模型,以及沒有辦法確定實驗前後的落差真的是實驗本身的影響,還是同時間有其他事件發生造成影響。為了解決時間序列法所造成的問題,2010 年後 MIT 的經濟學家發展了全新的方法 − 合成對造組 (Synthetic Control),將其他與研究目標高度相關個體的表現進行加權,編制出一個與研究目標表現高度相似的綜合指標,如下圖所示。比如說,在加州推行煙草法案後對於菸草銷量的影響,可以以全美其他州的煙草銷量編制指數。合成對照組的概念如右圖所示。
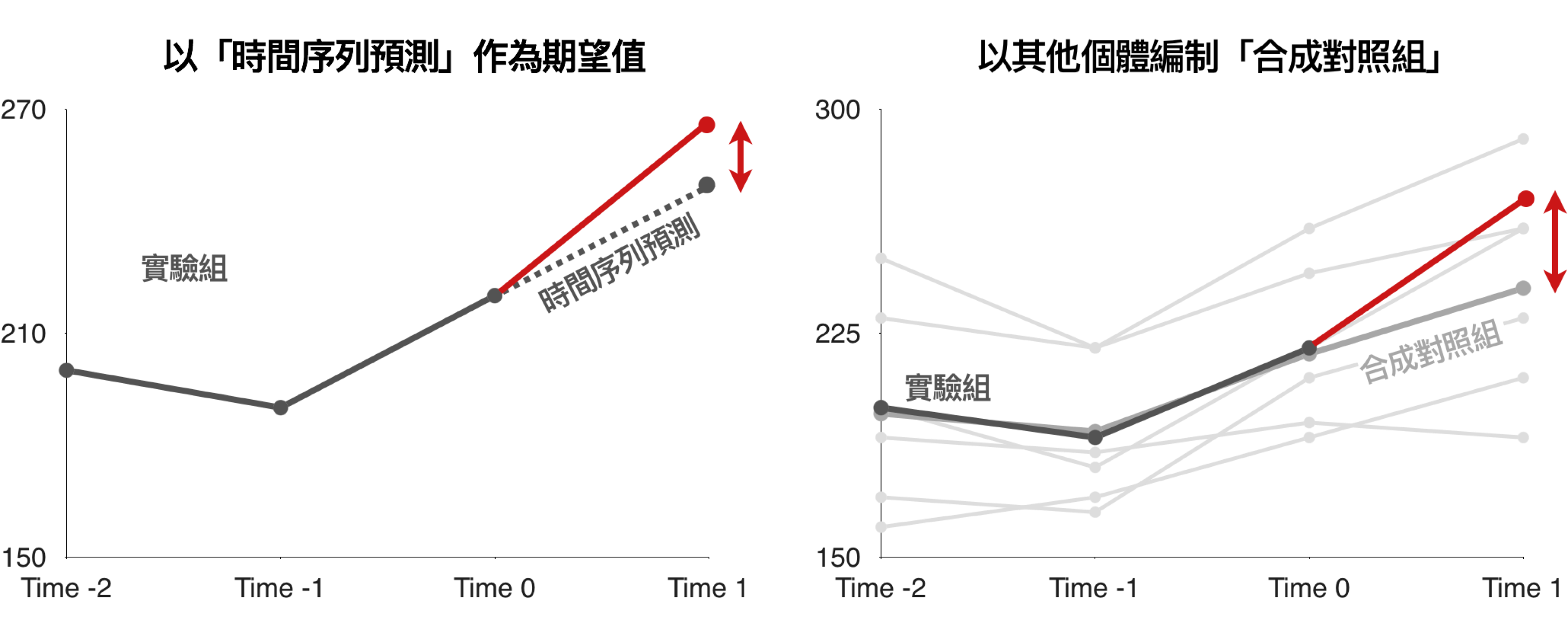
找出合成對照組:最簡單的方法永遠是最小平方法
假設個體 $latex 1$ 是唯一受到事件影響的個體,個體 $latex 2,~3,~\cdots, N$ 為可以被用來編制合成對照組的個體。此時,我們可以透過事件發生前的衡量指標來編制指數:令 $latex 1,~2,~\cdots,~ T_0$ 是事件發生前的時間點,個體 $latex i$ 在 $latex t$ 時點衡量指摽的數值為 $latex X_{it},~i=1,\cdots,N,~t=1,\cdots,T_0$,事件發生後個體 $latex i$ 衡量指標的數值為 $latex Y_i$。如此一來,我們可以將符號化簡為下列的表達方式:

編制與實驗個體衡量指標高度相似的合成指標,其實就是找出一組權重 ,使得在每一期編製出來的指標與實驗個體表先很相近,也就是
。為了達成這個目標,我們可以例用「極小化事件發生前合成對照組與實驗個體的誤差」來估計權重,也就是:
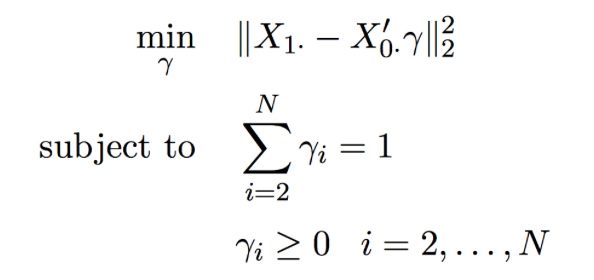
在這此處我們介紹的模型只有使用事件發生前衡量指標的數值進行編制,如果我們預先知道特定變數會影響衡量指標的話,也可以將這些變數納入決定衡量指標的範圍。另外,上述的最佳化過程其實有很多變形,比如說:如果有很多對照組候選,我們擔心過度配適 (overfitting) 的話,也可以加入 ridge 或是 lasso 的正規項,減少合成對照組的個體數量。
接著,我們便可以估計事件的成效,也就是:。你可能會覺得:這麼簡單就可以做好合成對照組嗎?答案是,如果我們在事件發生前的你和大部分情況這樣的方法都可以表現得不錯。然而,有時候利用事件發生前數據找到的合成對照組,與實驗組的相似度還是有所落差,這時可以加入時間序列預測,來幫助我們修正誤差,這樣的方法叫做 Augmented Synthetic Control,可以參考這篇論文。
案例:東西德合併對西德的影響
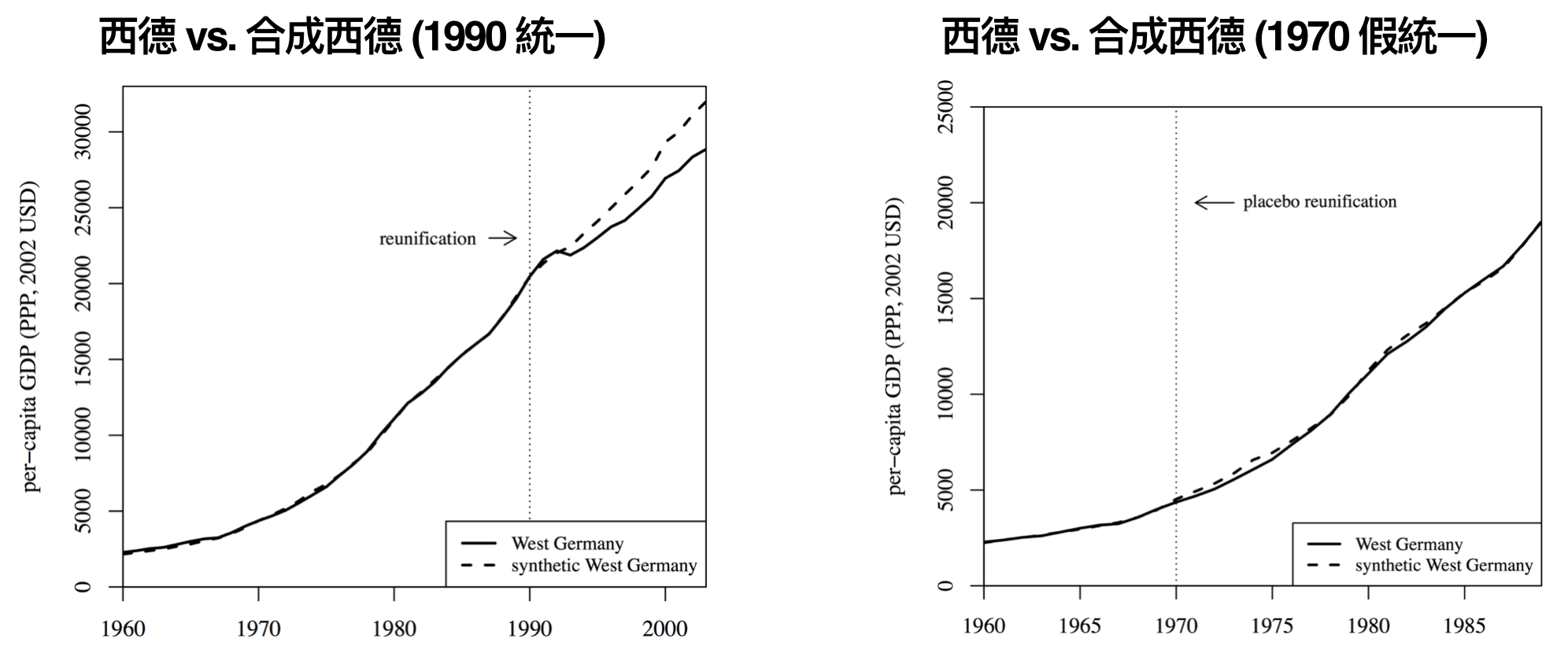
以東西德合併為例子,下列左圖是 1990 年東西德合併後西德與合成西德(利用 OECD 21 國所找出)的人均 GDP (GDP per capta) 落差。為了確保合成對照組的穩定性,我們也可以做一些模擬,比如說:假設隨機時點有事件發生(實際上並沒有),用時點前的資料找出合成對照組,並比較時點後實驗組與合成對照組是否有落差,如下列右圖所示。
有關 David’s Perspective 的最新文章,都會發布在大鼻的 Facebook 粉絲專頁,如果你喜歡大鼻的文章,還請您按讚或留言給我喔!
大鼻觀點:https://www.facebook.com/davidperspective/

感謝分享!我有兩個問題 ,1)怎麼選擇X vector中的特徵呢? intuitively,我覺得x應該是選取那些對y有strong predictive power的 2)怎麼選擇control region呢?即i = 1,…N 的這些region應該選取哪些?比如在東西德的例子中,我想一種方法是可以選所有其他的歐洲國家,但是,為什麼不把美國、亞洲國家也都加進去?每個individual control 是怎麼決定的呢?