今天想跟大家介紹的論文是 2019 年刊載在 The Annals of Statistics 的 Generalized Random Forest,將原本只用來預測 $latex Y_i$ 的隨機森林 (random forest) 推廣到任何種類的觀察值 $latex O_i$。這個架構非常適合估計異質處理效果 (heterogeneous treatment effect),以及任何待估計參數會受到個體特徵 (features) 影響的情況。這篇論文有個特別有趣的觀點,一是將隨機森林的結果當作 kernel,在估計時給予「與目標相似」的樣本點更多權重 (weights);二是在進行節點分割時,分割條件 (Splitting Criteria) 是「最大化兩個節點的異質性 (Heterogeneity)」,而不是 RSS、Gini Index 等常見指標。另外,這篇論文所提出的方法也有很好的統計表現,可以說是機器學習與因果推論結合的一大推進。
估計問題的定義
假設我們有一組 i.i.d. 的樣本 $latex i = 1, \cdots, N$,每一個觀察個體都有觀察值 $lates O_i$ 與共變量 (covariate) $latex X_i$,比如說:在一般迴歸的情況下 $latex O_i = Y_i$,有進行處置/實驗時 $latex O_i = \{Y_i, W_i\}$($latex W_i$ 是用來記錄處置類型),如果是工具變數 (instrument variable) 則 $latex O_i = \{Y_i, W_i,Z_i\}$。令我們有興趣的參數為 $latex \theta(x)$ (受到共變量的影響),而 $latex v(x)$ 為多餘參數 (nuisance parameter,如:簡單迴歸分析中的 $latex \alpha$)。此處採用很常見的參數估計技巧:
假設參數 $latex \theta(x)$ 與 $latex v(x)$ 滿足 $latex \mathbb{E}\left(\psi_{\theta(x),v(x)}(O_i)|X_i = x\right)=0,~~\forall x \in \mathcal{X}$,其中 $latex \phi(\cdot)$ 是某個評分函數 (Scoring Function)。
以分量迴歸 (quantile regression) 為例子,假設我們想估計的是給定 $latex X_i = x$,$latex Y$ 的分量 $latex q$,在此處 $latex \theta(x) = F^{-1}(q),~q\in [0,1]$,其中 $latex F$ 是 $latex Y|X$ 的累積分配函數 (cumulative distribution function),而評分函數可以訂為 $latex \psi_{\theta(x),v(x)}(Y_i) = q \mathbf{1}(\{Y_i > \theta (x)\}) – (1-q) \mathbf{1}(\{Y_i \leq \theta (x)\})$。
以 Forest 為基礎的局部估計
在實際資料集合上進行估計時,可以採取「局部估計法」(local estimation):
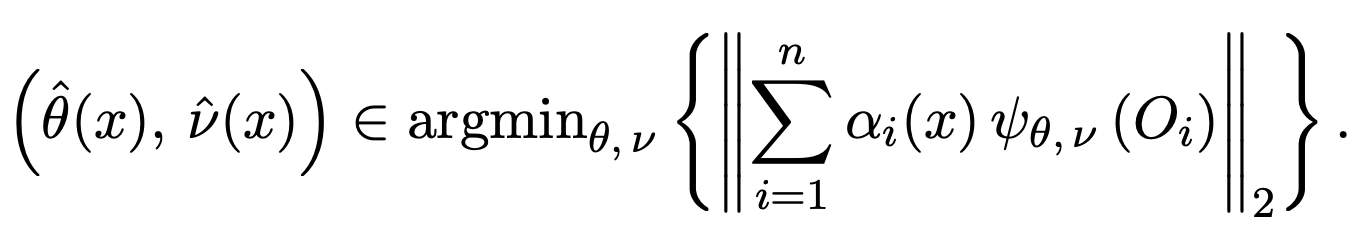
其中 $latex \alpha_i(x)$ 就是用來調節第 $latex i$ 個樣本對於 $latex \theta$ 的貢獻程度。換句話說,給定共變量 $latex X=x$,我們想決定哪些樣本點比較適合用來估計 $latex \phi(x)$,因此針對每個樣本點都 $latex i = 1, \cdots, N$ 給定 $latex \alpha_i(x)$,而 $latex \alpha_i$ 越大,代表該樣本貢獻給待估計參數的資訊量越多。
這篇論文採用類似「隨機森林」的方式來決定這個權重。首先,透過重抽樣 (resampling / bootstraping) 訓練 $latex B$ 個迴歸樹。對於第 $latex b$ 棵樹而言,將與 $latex x$ 落在同一個節點 / leaf 的樣本點所形成的集合計為 $latex L_b(x)$,而 $latex |L_b(x)|$ 代表這棵樹分類與 $latex x$ 落在同一個節點的樣本點個數。
假設在這棵樹中總共有 10 個樣本點落在與 $latex x$ 相同的節點,對於這些樣本設定他們貢獻給 $latex \theta(x)$ 的貢獻為 1/10,其他樣本點的貢獻度則為 0,因而得到這棵樹第 $latex i$ 個樣本點的去中 $latex \alpha_{bi}(x)$。接著,我們將每棵樹得到的權重做平均,得到最終的權重 $latex \alpha_i(x)$ ,以數學公式表示為:
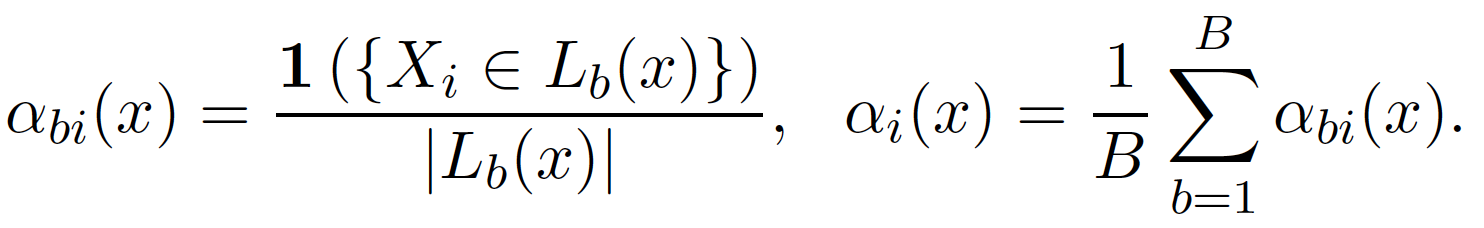
這樣的過程可以由下面的示意圖表示,上面的每一個小圖都是一個迴歸樹的訓練結果,藍點是我們希望用來估計參數的 $latex x$,比較大的黑點則是與 $latex x$ 落在同一個節點的樣本點。將這些小樹得到的權重做平均,最後就可以得到最下方的結果,其中黑點的大小就代表最後得到該樣本點的權重。
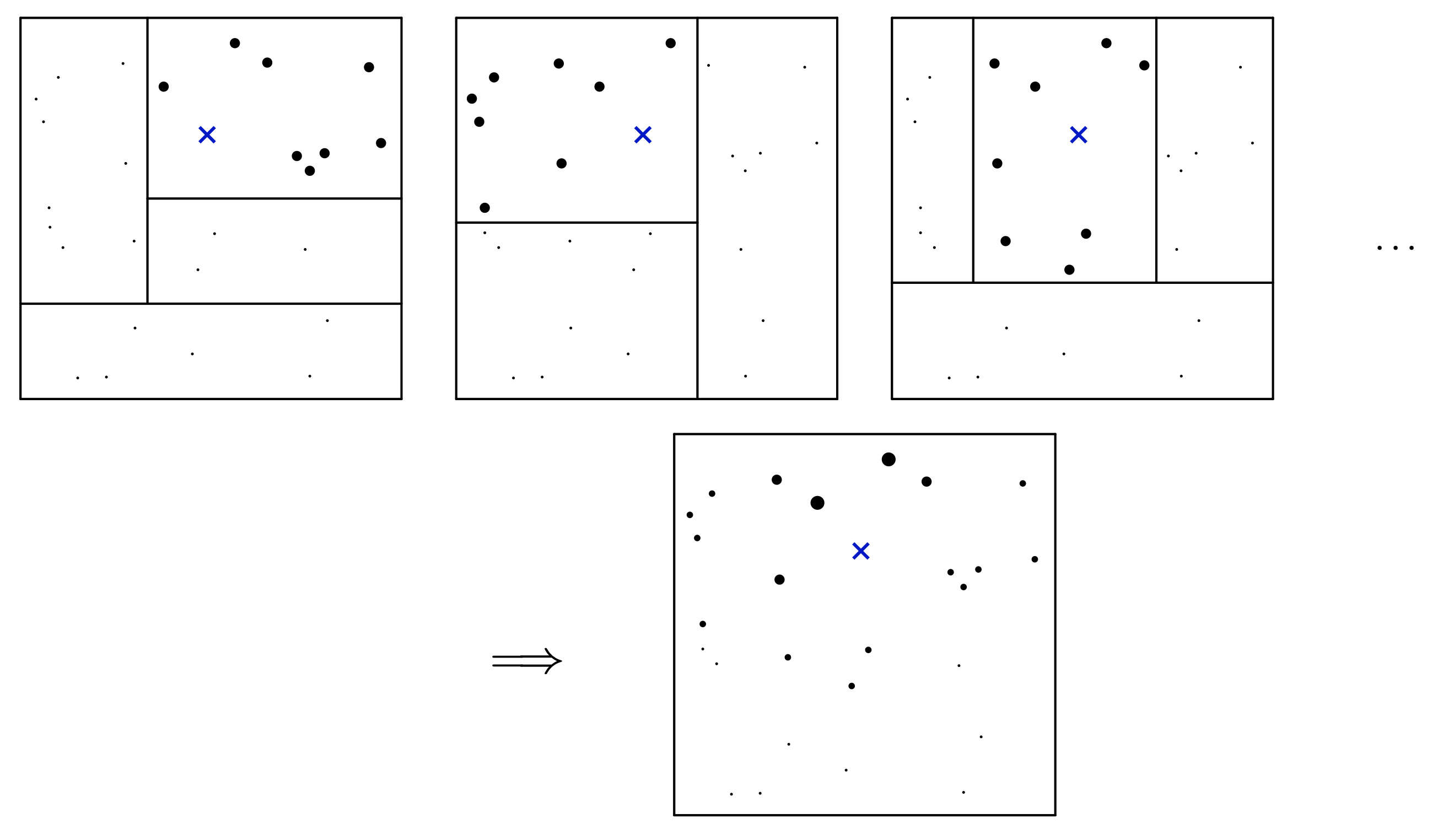
以「最大化異質性」為分枝條件
由於我們的目標是能夠準確估計參數 $latex \theta(x)$,因此在每一個樹進行節點分枝的時候,我們的目標不再是 impurity measure 或 RSS,而是能夠使分枝出兩個節點估計的參數能夠越準確越好。首先,針對單一節點 $latex P$ 與一組樣本資料 $latex \mathcal{J}$,我們估計參數 $latex \theta, v$ 的方法是:
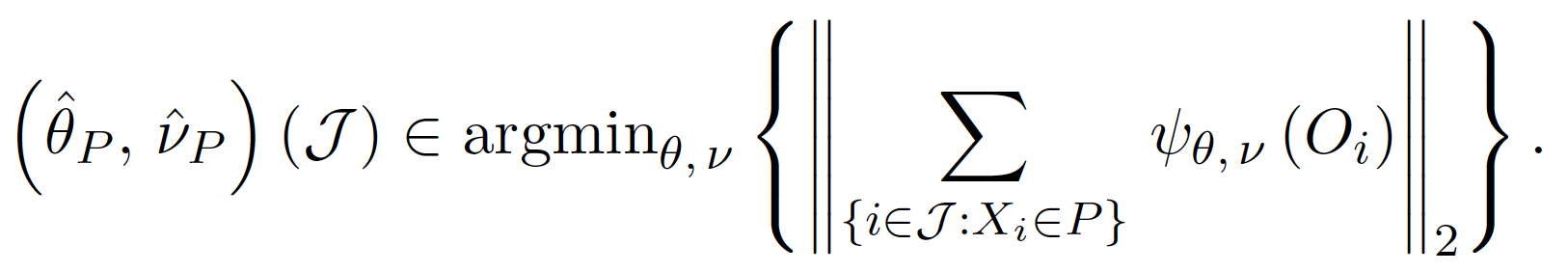
接著,我們要將節點 $latex P$ 分為兩個子節點 $latex C_1, C_2$。在此處我們分割的目標是極小化參數估計的誤差,也就是極小化:
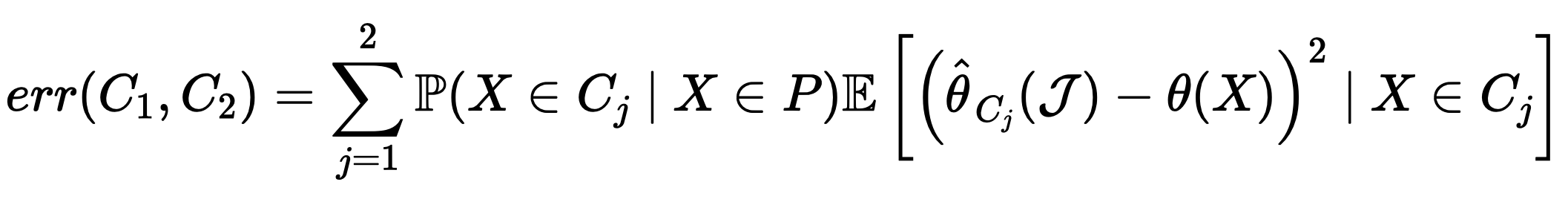
實際上將這個誤差函數拆解後(論文中的 Proposition 1),我們會發現極小化 $latex err(C_1,C_2)$ 跟極大化下面的函數等價:
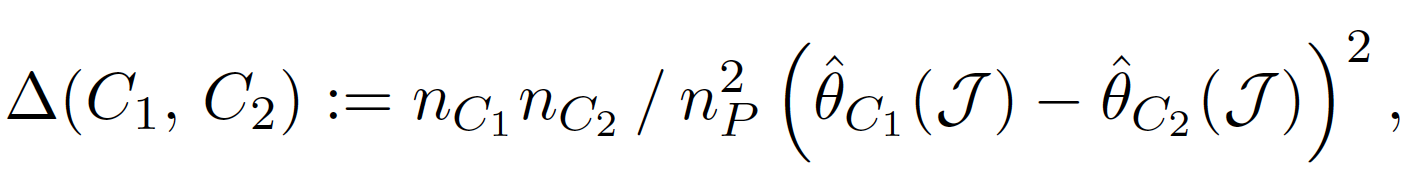
此處「極小化估計誤差」與「極大化兩個節點間的參數差異」其實是等價的,也就是說,在進行分枝時,可以以「極大化兩個節點的異質性 (Heterogenity)」為分枝條件。
利用 Gradient Tree 估計參數
想直接利用全域搜尋的方法解決上面的極小化 $latex \widehat{\theta}_P, \widehat{v}_P$ 與極大化 $latex \Delta(C_1,C_2)$ 問題其實不大可行,運算成本會非常高,因此可以使用 Gradient 逼近的方式簡化計算。首先,我們先計算出 $latex \nabla\mathbb{E}\left(\psi_{\widehat{\theta}_{P},\widehat{v}_{P}}(O_i)|X_i\in P\right)$ 的一致估計式 (consistent estimator),計為 $latex A_P$。比如說,如果評分函數 $latex \phi$ 是連續可微分函數,那麼 $latex A_P$ 的為:
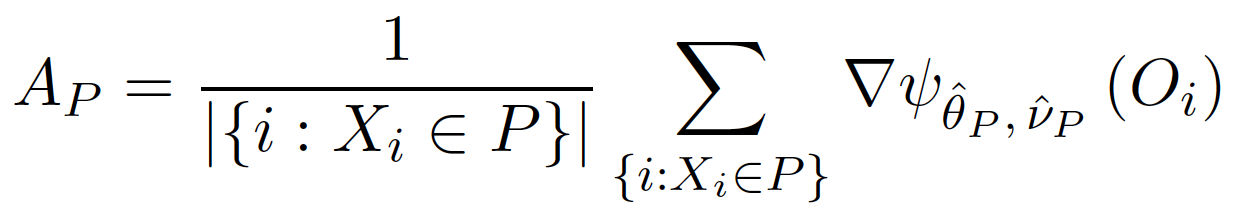
接著,我們可以得到 $latex \widehat{\theta}_C$ 的近似解為
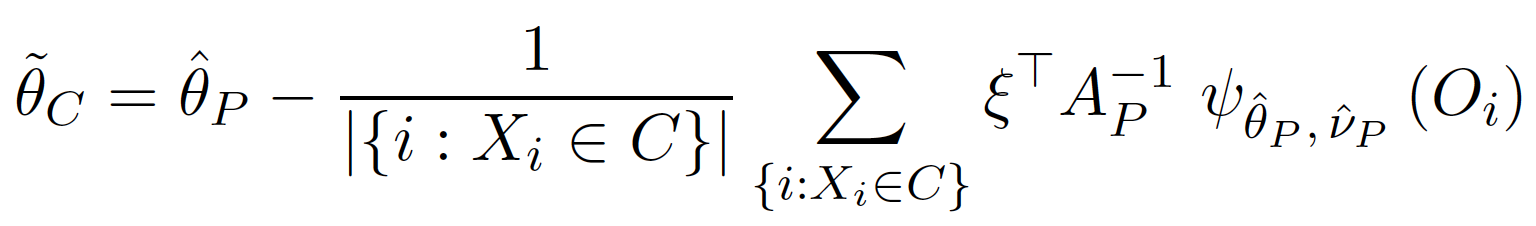
其中 $latex \xi$ 向量可以將 $latex \phi$ 與 $latex \theta$ 有關的元素抽取出來。
從上述的推導,我們可以設計 Gradient tree 的演算法:在標記步驟 (labeling stage) 時,我們先在母節點 (parent node) 計算出 $latex \widehat{\theta}_P, \widehat{v}_P, A^{-1}_P$,並針對每個樣本點 $latex i$ 計算出虛擬的目標值:
![]()
接著,我們可以進行節點分枝 (splitting),此時分枝條件為極大化以下的函數:
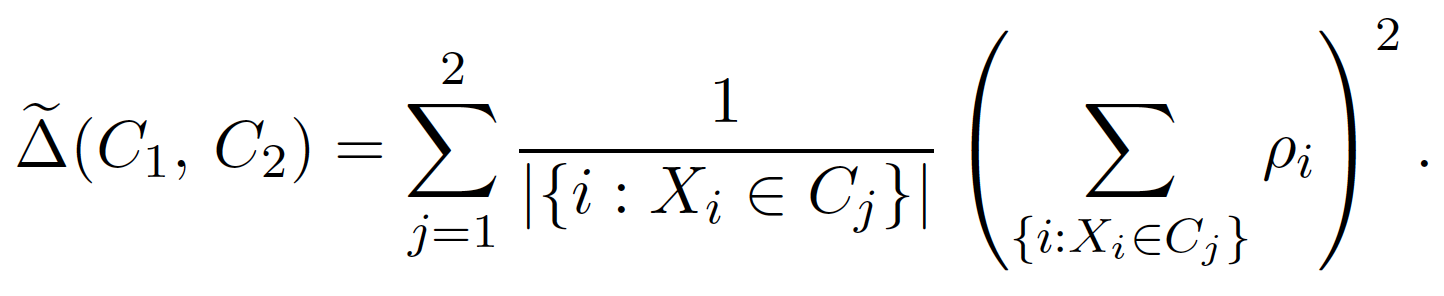
以最簡單的迴歸分析問題為例,此時 $latex \phi_{\theta(X)}(Y_i) = Y – \theta(X)$,此時 $latex \rho_i = Y_i – \overline{Y}_P$,而分枝條件則會變成與原本隨機森林函數中一致。
GRM 演算法
最後,將上述的各個元素整合在一起,就可以得到以下一般化隨機森林 (Generalized Random Forest) 的演算法。這個估計方法在一些不算嚴格的條件下有很好的統計性質:一致性 (consitency) 與漸進常態 (asymptotic normality),因此也可以透過 delta-method 估計出參數 $latex \theta(X)$ 的信賴區間。 

有關 David’s Perspective 的最新文章,都會發布在大鼻的 Facebook 粉絲專頁,如果你喜歡大鼻的文章,還請您不吝嗇地按讚或留言給我喔!

好奇問一下,是否在網路上有看到測試這個模式的文章呢?感謝!
我只知道有 R 的套件~
https://grf-labs.github.io/grf/