消除估計偏誤的雙重機器學習 (Double Machine Learning)

今天想要跟大家分享一篇很有趣的論文— Double/Debiased Machine Learning for Treatment and Structural Parameters，用來衡量政策的成效。假設我們想要估計一項 $10 M 的行銷計畫對于消費者的影響，因此定義 outcome variable $latex Y$ 為消費者在行銷計畫期間的消費金額，此時我們常會使用一種叫做 Partially Linear Model 的建模方法。

當期消費 $latex Y$ 可能有幾種不同的影響因素：一是消費者本身對我們公司產品的消費潛力以及喜好，假設這些因素可以用一組代理變數 $latex \mathbf{Z}$ 來表示；第二個是跟行銷計畫有關，令計劃的成效變數是 $latex \theta_0$，也就是我們估計的目標；第三，這個行銷計畫的成效可能會跟過去的消費分數有關，因此我們將這個與計畫成效有關的分數令定義為 $latex D$，比如說：$latex D = \sum_{t=1}^{T-1} Spend_t$ 是過去消費計畫的總和。在上面的論述下，我們會寫出模型：$latex Y=D\cdot\theta_0+g_0(\mathbf{Z})+U,~~\mathbb{E}(U|\mathbf{Z},D)=0 $。之所以叫做 Partially Linear Model，是因為政策的影響 $latex D\cdot\theta_0$ 跟原本的預期消費水準 $latex g_0(\mathbf{Z})$ 是線性關係，但 $latex g_0$ 可以是非線性函數。

機器學習模型引入的偏誤

傳統上用來估計 Partially Linear Model 的方法是交替最小化 (Alternative Minimization)，也就是：

1. 設定 $latex \theta_0$ 的初始值 $latex \widehat{\theta_0}^{(0)}$
2. 建立 $latex \mathbf{Z} $ 與 $latex Y –  D \widehat  {\theta_0}^{(0)}$ 之間的機器學習模型，以估計 $latex \widehat{g_0}^{(1)}$
3. 建立$latex D$ 與 $latex Y-  \widehat{g_0}^{(1)}(\mathbf{Z})$ 之間的線性迴歸，以估計 $latex \widehat{\theta_0}^{(1)}$
4. 重複上列估計方法，直到 $latex |\widehat{\theta_0}^{(i)}-\widehat{\theta_0}^{(i-1)}|<\epsilon$ 收斂，得到最終的估計$latex \widehat{g_0}$ 與 $latex \widehat{\theta_0}$

上面這個估計是最大的問題在於： $latex \widehat{\theta_0}$ 就算樣本數 $latex N$ 很大，但因也不會機率收斂到 $latex \theta 0$。如何得到收斂速度呢？首先，我們透過線性迴歸，可以得到最小平方法 (OLS) 下的估計式：

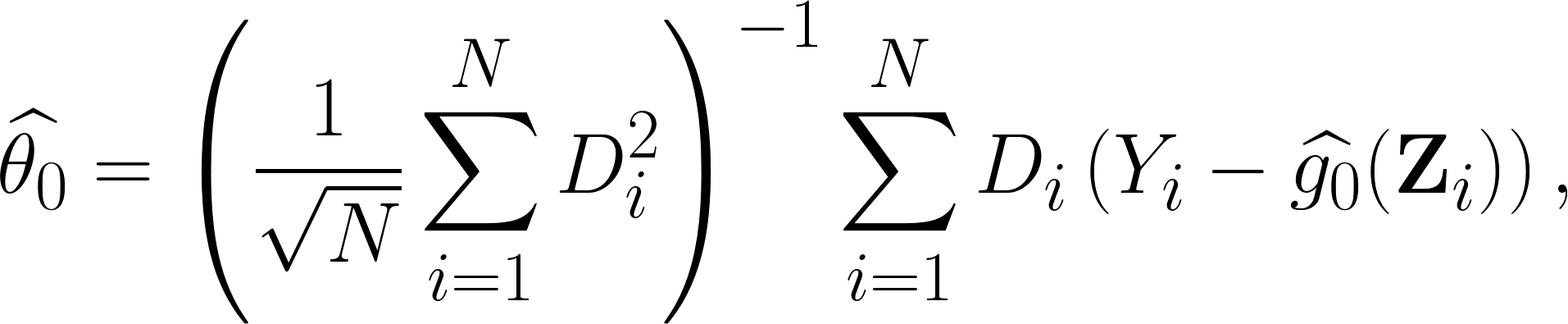
由上是我們可以得到以下估計誤差：

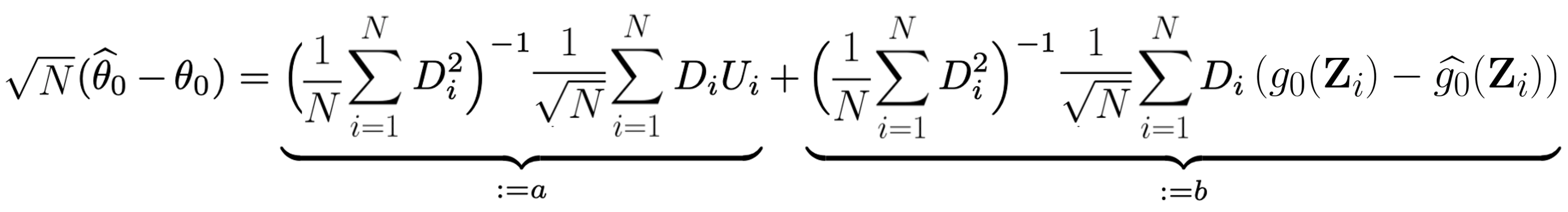
其中 $latex a$ 因爲 $latex U_i$ 的性質會機率收斂到 0，但 $latex b$項因為 $latex g_0  – \widehat{g_0}$ 的期望值通常不等於 0（因為引入了 $latex D\theta_0$ 項），因此整項隨著 $latex N$ 趨近於無限大時，其實是會發散的，因而造成 $latex |\sqrt{N}(\widehat{\theta_0} – \theta_0)| \rightarrow_P \infty$。就算機器學習模型沒有偏誤，但 $latex b$ 項的收斂速速也會慢於 $latex O_P(\sqrt{N})$，因此不是很好的估計式。

雙重機器學習方法 (Double Machine Learning)

為了解決上述 $late b$ 項的收斂問題，論文中提出了新的做法：同時建立 $latex g_0$ 與 $latex D$ 的機器學習模型，來校正 $latex \theta_0$ 的估計，而此處的概念，是來自初等計量經濟學可能會學到的 Frisch–Waugh–Lovell 定理：估計 $latex X_1, \cdots, X_p$ 與 $latex Y$ 的線性迴歸模型，其實可以想成以下步驟：

1. 估計 $latex X_1$ 與 $latex X_2, \cdots, X_p$ 間的線性迴歸，得到殘差 $latex \widehat{V}$
2. 估計 $latex Y$ 與 $latex X_2, \cdots, X_p$ 做線性迴歸，得到殘差 $latex \widehat{U}$
3. 估計 $latex \widehat{U}$ 與 $latex \widehat{V}$的線性迴歸模型

此處我們可以將原本的 Partially Linear Model 寫作以下形式：

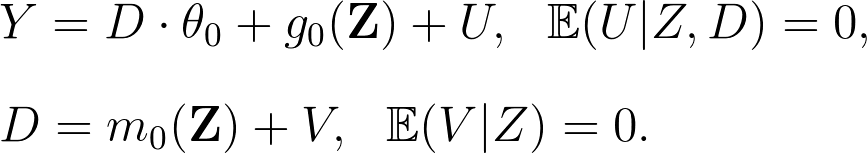
在估計的時候，我們可以採用類似上面 Frisch–Waugh–Lovell 的估計方法：

1. 建立機器學習模型 $latex \widehat{D} = \widehat{m_0}(\mathbf{Z})$，得到殘差 $latex \widehat{V}$
2. 利用用 Alternative Minimization 建立 $latex \widehat{Y} = D\widehat{\theta_0} + \widehat{g_0}(\mathbf{Z})$，得到殘差 $latex \widehat{U}$
   (如果是利用 Frisch–Waugh–Lovell 類型的估計式，則可以直接建立 $latex \widehat{Y} = \widehat{l_0}(\mathbf{Z})$ 模型)
3. 建立 $latex \widehat{U}$ 與 $latex \widehat{V}$ 的簡單迴歸模型，得到係數為 $latex \widetilde{\theta_0}$

此時，我們得到的估計式  $latex \widetilde{\theta_0}$ 為：

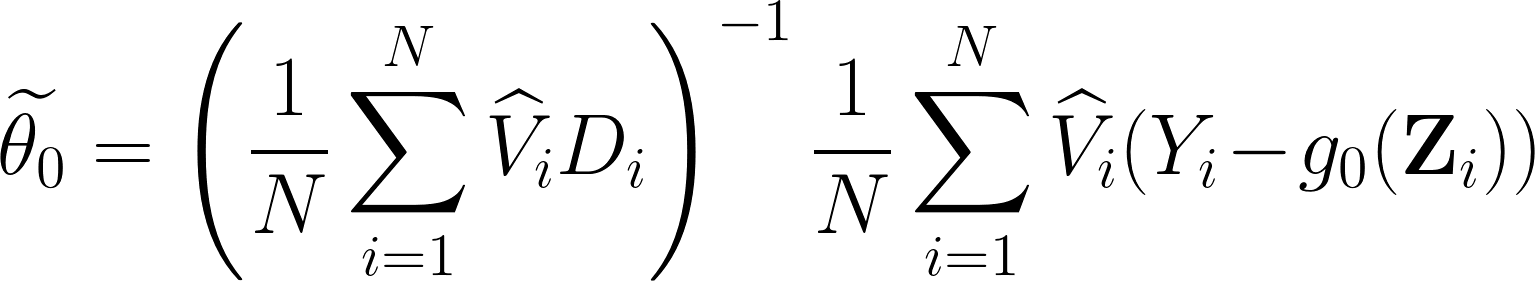
通樣的，為了得到收斂速度的分析，我們可以再度進行分解 $latex \sqrt{N}\left(\widetilde{\theta_0} -\theta_0\right) = a’ + b’ + c’$，其中：

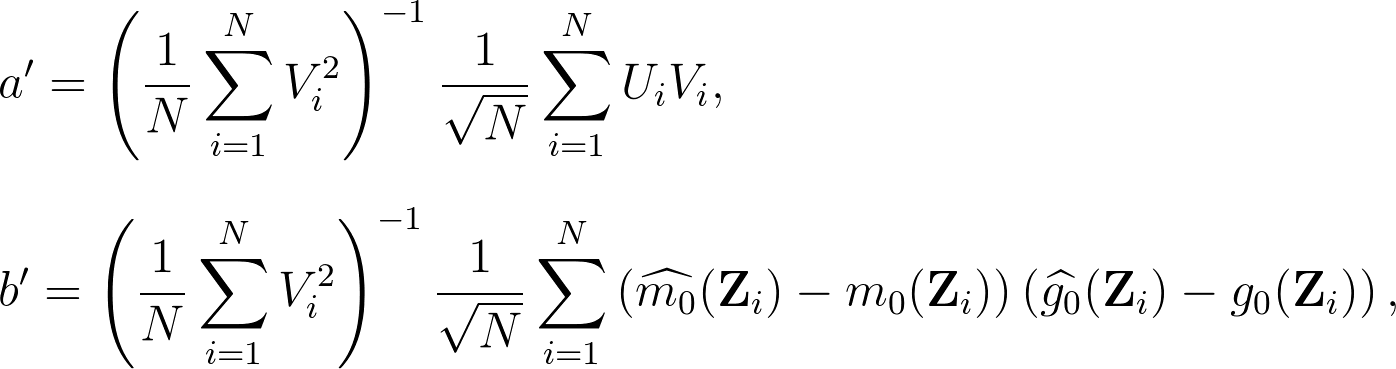
其中 $latex a’$ 的在一些很寬鬆的動差條件下就會收斂，$latex  b’$ 因為加入了 $latex \left(\widehat{m_0}(\mathbf{Z}_i) – m_0(\mathbf{Z}_i)\right)$  項，所以很容易收斂到 0 （當使用夠複雜的機器學習模型估計），因此雙重機器學習的技巧可以確保本來會出問題的 $latex b$ 項 (Regularization Bias) 不會發散。下圖則在模擬實驗比較了採納「雙重機器學習」跟沒有採納的結果：

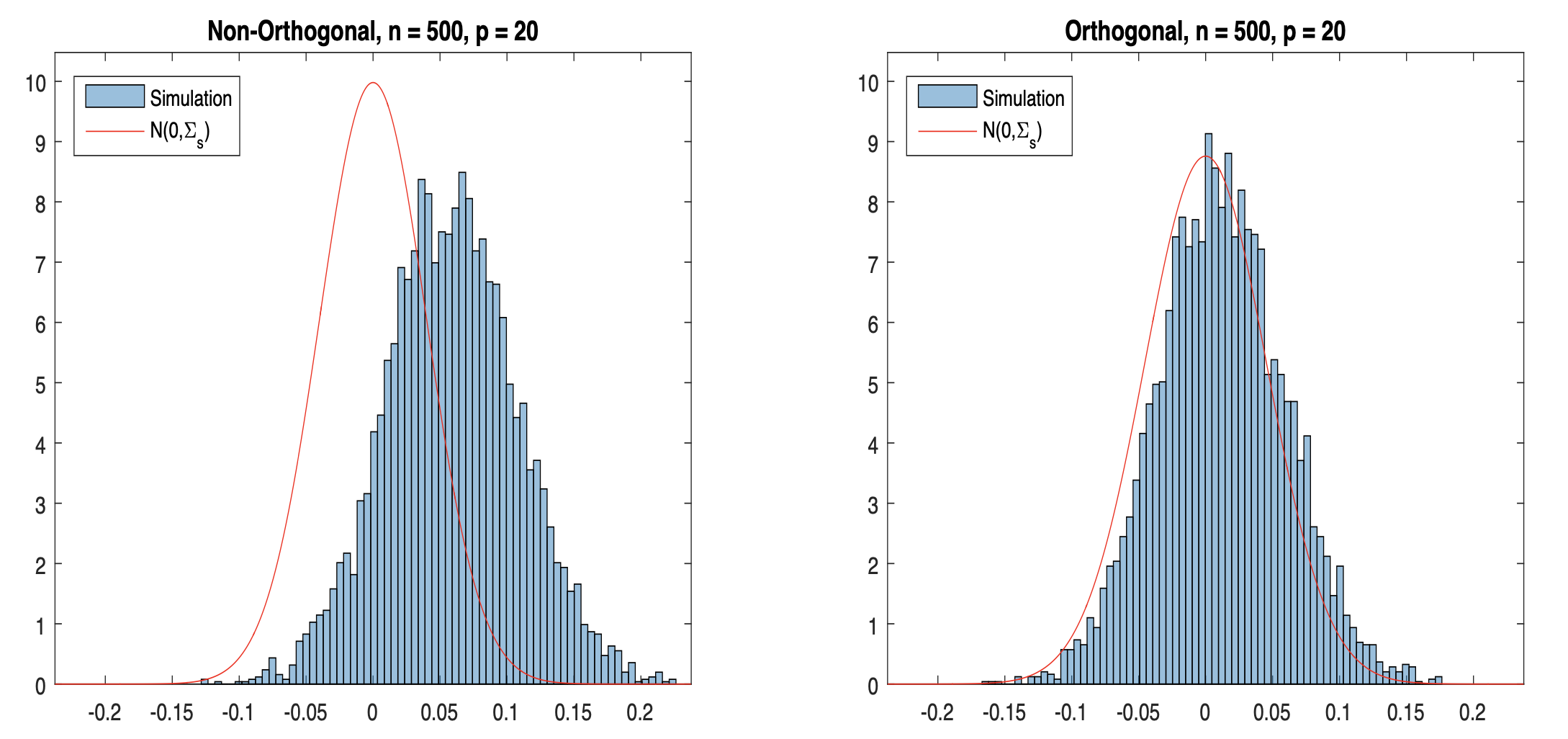
樣本分割 (Sample Splitting) 與交互配適 (Cross-fitting)

上面雖然解決了然而 $latex c’$ 中其實包含了 $latex \frac{1}{\sqrt{N}}\sum_{i=1}^N V_i\left(\widehat{g_0}(\mathbf{Z}_i) – g_0(\mathbf{Z}_i)\right )$， 這項如果在 $latex V_i$ 與 $latex \widehat{m_0}, \widehat{g_0}$ 之間產生相關性的話，就不會收斂了。什麼時候會產生這種情況呢？很大有可能是在模型訓練的過程中，$latex \widehat{m_0}, \widehat{g_0}$ 可能會為了確保 $latex Y$ 的預測準確性，而不小心摻入了 $latex D\theta_0$ 的資訊，也就代表 $latex \widehat{m_0}, \widehat{g_0}$ 與  $latex V$ 有關，另外也可能是本來兩種誤差 $latex U,V$ 本來就不獨立，而模型在確保 $latex Y$ 的預測準確性可能也會摻入 $latex U$ 的資訊，因此造成 $latex c’$ 不會收斂到 0，這樣的偏誤也因此被叫做 Overfitting Bias。

要確保這樣的情況不會發生，其實可以透過樣本分割的方式來處理：如果估計 $latex \widetilde{\theta_0}$ 跟估計 $latex \widehat{m_0}, \widehat{g_0}$ 的樣本不一樣，就可以確定 $latex V_i$ 與 $latex \widehat{g_0}$ 不會相關了。因此，我們可以進行下列的演算：

1. 將樣本隨機分成兩組 $latex I$ 與 $latex I^c$
2. 利用樣本 $latex I$ 建立機器學習模型 $latex \widehat{D} = \widehat{m_0}(\mathbf{Z})$
3. 利用樣本 $latex I$ 建立 $latex \widehat{Y} = D\widehat{\theta_0} + \widehat{g_0}(\mathbf{Z})$
4. 利用上述得到的 $latex \widehat{g_0}$ 與 $latex \widehat{m_0}$，在樣本 $latex I^c$ 上得到殘差項 $latex \widehat{U}^c$ 與 $latex \widehat{V}^c$ ，透過簡單迴歸模型，得到係數為 $latex \widetilde{\theta_0}$

下圖是採納了樣本分割與沒有採納的結果：

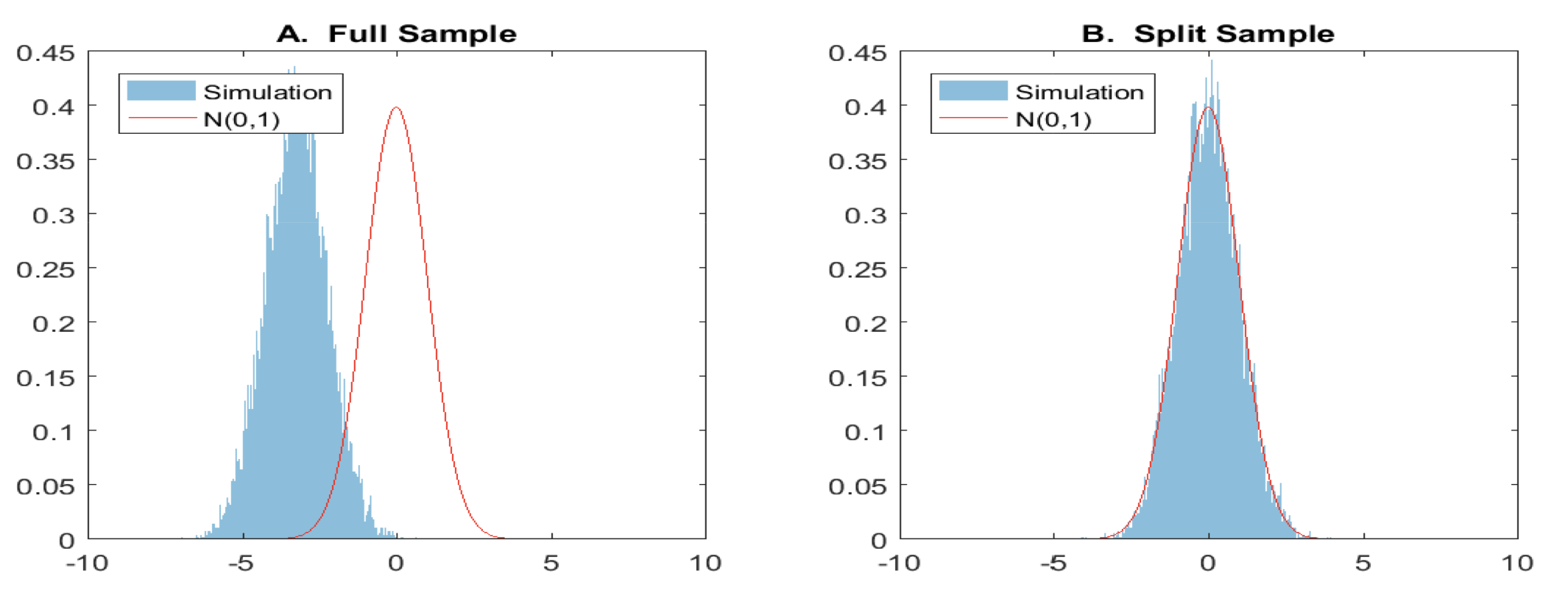
這樣我們終於可以得到 $latex \theta_0$ 的 $latex sqrt{N}$ 的一致估計式了！然而上述的演算法最大的缺點就是：可能會失去大量的資訊（因為將樣本切割的關係），因此我們可以在做交互配試 (Cross Fitting)：

1. 將樣本隨機分成兩組 $latex I$ 與 $latex I^c$
2. 利用樣本 $latex I$ 建立機器學習模型 $latex \widehat{m_0}^{(0)}$ 與 $latex \widehat{g_0}^{(0)}$
3. 利用  $latex \widehat{m_0}^{(0)}$ 與 $latex \widehat{g_0}^{(0)}$ 在 $latex I^c$ 得到殘差項，並估計 $latex \widetilde{\theta_0}^{(0)}$
4. 利用樣本 $latex I^c$ 建立機器學習模型 $latex \widehat{m_0}^{(1)}$ 與 $latex \widehat{g_0}^{(1)}$
5. 利用  $latex \widehat{m_0}^{(1)}$ 與 $latex \widehat{g_0}^{(1)}$ 在 $latex I$ 得到殘差項，並估計 $latex \widetilde{\theta_0}^{(1)}$
6. 得到最後的估計目標  $latex \widetilde{\theta_0}=\frac{\widetilde{\theta_0}^{(0)}+\widetilde{\theta_0}^{(1)}}{2}$

基於這個案例，作者在後面開始正式定義上面提到的種種觀念以及一般化的 DML，以及如何從 DML 去得到 Average Treatment Effect 與 Local Treatment Effect，有興趣的朋友可以仔細去讀讀這篇論文喔！

有關 David’s Perspective 的最新文章，都會發布在大鼻的 Facebook 粉絲專頁，如果你喜歡大鼻的文章，還請您不吝嗇地按讚或留言給我喔！

大鼻觀點：https://www.facebook.com/davidperspective/