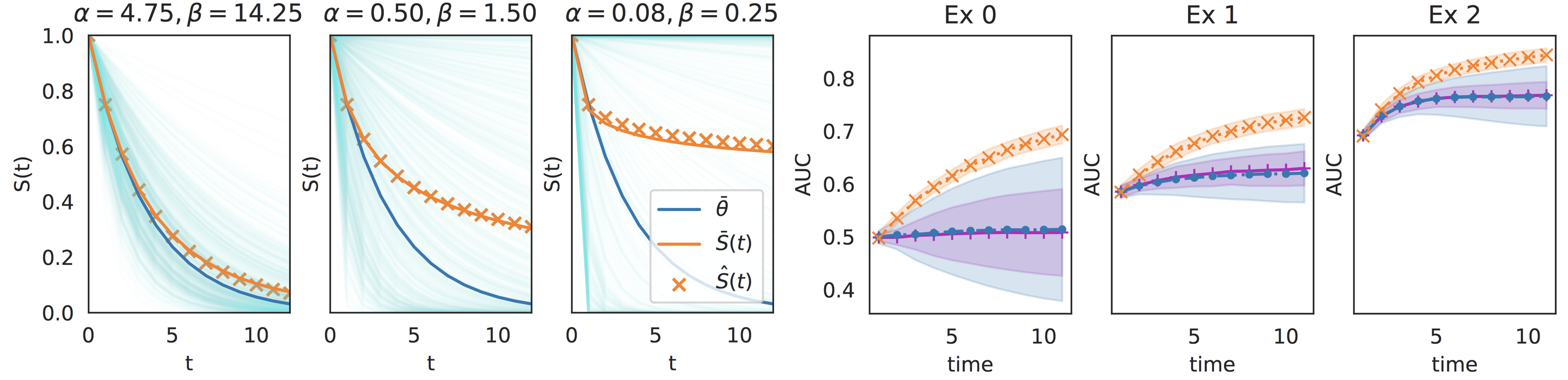
最近在研究客戶留存的問題時,看到了 Netflix 的一篇有趣的文章:Beta Survival Models。在這篇文章中,他們將留存模型 (retention modeling) 中很經典的 Shifted Beta-Geometric Model 與用戶的特徵 (feature/covariates) 連結在一起,做出挺有趣的參數化方法,估計個別用戶的留存機率。
Shifted Beta Geometric Model
假設使用者(其特徵為 $latex \mathbf{x}$)在每個離散時間點(比如說:每一期繳費前)$latex t$ 會決定是否要繼續訂閱 Netflix 服務,其中用戶取消訂閱的機率為 $latex \theta$、持續訂閱的機率為 $latex 1 – \theta$,而且 $latex \theta$ 會隨著使用者的特徵不同而改變(也就是指:$latex \theta$ 是 $latex \mathbf{x}$ 的函數),比如說:第一個月用觀看時間越長的用戶,取消訂閱的機率 $latex \theta$ 就越小。令 $latex T$ 代表用戶取消訂閱的時間,則 $latex T$ 的機率分配為幾何分配 (Geometric distribution),其機率質點函數 (probability mass function) 為:
![]()
上式是怎麽得到的呢?其實很簡單,假設用戶在第 $latex t$ 期取消訂閱,代表在第 $latex 1,2,\cdots, t-1$ 期用戶都沒有取消,機率為 $latex (1-\theta)^{t-1}$,而在在第 $latex t$ 期取消的機率是 $latex \theta$,因此我們可以得到上式。
如果有學過貝式統計,應該不陌生,通常我們會使用 Beta 分配來描述 Bernoulli 機率,因此,在這裡我們設定 $latex \theta$ 的條件分配 (conditional distribution) 為 $latex B(\alpha (\mathbf{x}), \beta (\mathbf{x}))$ 分配,也就是說,此處透過 Beta 分配中的 $latex \alpha, \beta$ 來連結 churn probability 與使用者特徵的關係。因此,我們可以寫下 $latex \theta$ 的條件機率密度函數 (conditional density function) 為:
![]()
其中 $latex \alpha (\cdot), \beta (\cdot)$ 皆為大於 0 的函數。為了確保大於 0 的條件,比較好的方法是將其參數化為 $latex \alpha(\mathbf{x}) = \exp a(\mathbf{x}) , \beta(\mathbf{x}) = \exp b(\mathbf{x})$,目標則轉變成估計 $latex a, b$ 函數。
接下來,我們可以透過 MAP (maximum a posterior) 方法估計 $latex \alpha, \beta$。令 $latex c_i = 0$ 代表使用者 $latex i$ 再觀察時間內有退訂 (c 代表 censored)且退訂時間記為 $latex t_i$,$latex c_i = 1$ 代表沒有退訂且最後訂閱的時間記為 $latex t_i$,則我們可以將 $latex \alpha, \beta$ 的後驗分配寫為:
![]()
其中 $latex \mathbb{P}\left(T = t_i|\alpha(\mathbf{x}_i),\beta(\mathbf{x}_i)\right) =\int_0^1f\left(\theta|\alpha(\mathbf{x}_i),\beta(\mathbf{x}_i)\right)\mathbb{P}(T=t_i|\theta)d\theta$。
利用遞迴關係估計 $latex \alpha, \beta$
接下來,我們要透過 Gamma 函數的性質,寫出遞迴形式,透過遞迴形式,我們可以更進一步得到遞迴形態的 gradient,幫助我們解出後驗分配的最大化問題。首先,我們列出起始條件,也就是 $latex t = 1$ 的情況(此處為求符號簡單,省略 $latex \mathbf{x}_i$):
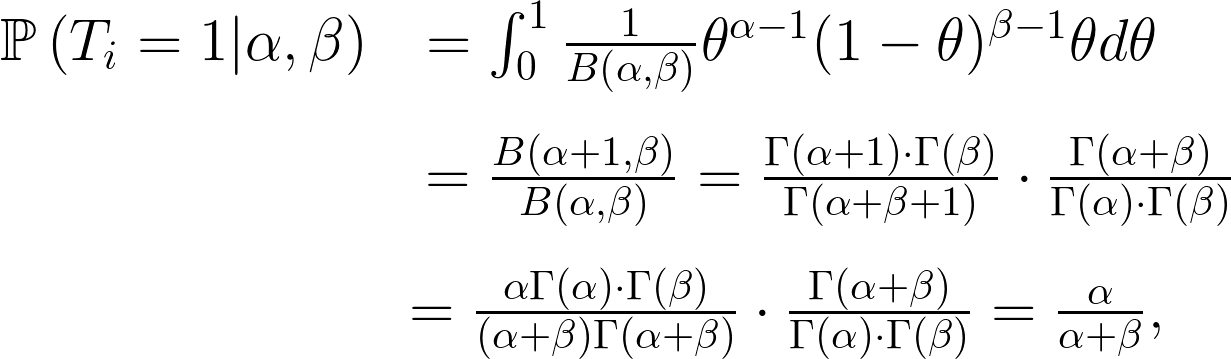
![]()
透過類似的技巧,我們可以得到以下的遞迴形式:
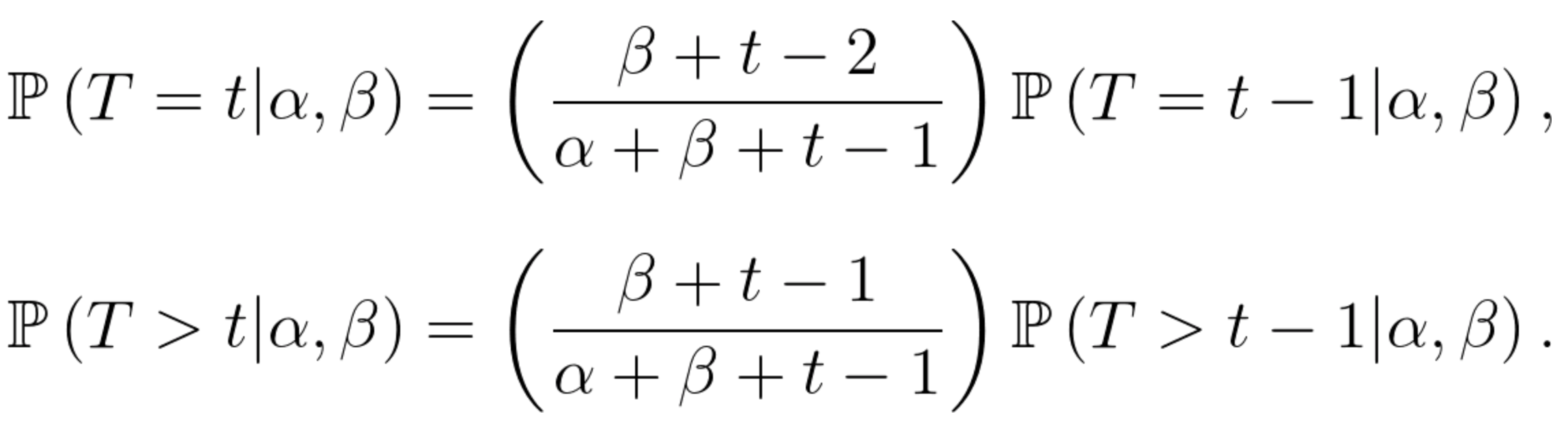
有了上述的遞回形式,針對每個用戶 $latex i$,我們都可以從 $latex t = 1$ 計算到 $latex t = t_i$,得到概似函數 $latex \mathbb{P}(T > t_i|\alpha,\beta)$ 或是 $latex \mathbb{P}(T = t_i|\alpha,\beta)$。
接下來,我們要透過 MAP 估計 $latex \alpha,\beta$,也就是求解最佳化問題 $latex \max_{\alpha,\beta} \mathcal{L}(\alpha,\beta) \equiv \min_{\alpha,\beta} -\log\mathcal{L}(\alpha,\beta)$,其中損失函數 (loss function) 的形式為:
![]()
此處我們可以透過上述的遞迴形式以及簡單的微積分,就可以得到如論文 Appendix 2 中的遞迴式,也可以順利計算出 Gradient 和 Hessian 的數值。因此,此處我們已經可以順利計算出 loss function, Gradiient, Hessian 的數值,因此就有辦法透過 Gradient Descent 方式解出 $latex \alpha, \beta$ 了。
Beta-logistic 模型
上述的 Beta 存活模型,最簡單的形式便是假設線性關係,也就是 $latex a (\mathbf{x_i})=\gamma_a \cdot \mathbf{x_i}, b (\mathbf{x_i})=\gamma_b \cdot \mathbf{x_i}$,此時我們可以發現在 $latex t = 1$ 時:
![]()
變成了邏輯迴歸的連結函數 (link function),因此作者將這個簡化的模型稱為 Beta-logistic 模型。在論文中還有再提到幾個面向的討論,一是比較兩個使用者的流失機率:
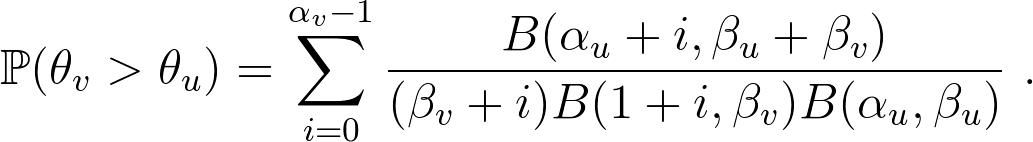
另一個面向則是 Posterior Size Comparision,也就是比較估計出 $latex \theta$ 的信賴區間大小。
這篇論文運用貝式統計進行參數估計與預測的方法其實很經典,但滿巧妙的連結了離散事件跟使用者特徵,而且並不一定只適用於線性模型,比較複雜的方法也可以用來參數化 $latex \alpha, \beta$,論文本身的數學難度也不高,滿建議修過貝氏統計的朋友可以讀一讀!有關 David’s Perspective 的最新文章,都會發布在大鼻的 Facebook 粉絲專頁,如果你喜歡大鼻的文章,還請您不吝嗇地按讚或留言給我喔!