之前我朋友在找機器學習相關的工作時,遇到一到面試問題:「主成份分析」(principal component analysis) 與「嶺迴歸」 (ridge regression) 之間有什麼關係?當下他有點困惑的來詢問我兩者之間哪裡有關,後來想想好像很少有機器學習的課程會談到這件事 (畢竟一學期的課程要上這麼多內容,很難討論到這麼細節的性質),因此我想跟大家討論一下這兩者之間的關連。
回顧:迴歸分析與最小平方法
針對 $latex n$ 個個體我們蒐集了變數 $latex X_1, \cdots, X_p$ 與 $latex Y$ 的相關資料,我們會得到以下資料矩陣:
,
。
為求方便,不失一般性地假設$latex X_1, \cdots, X_p$ 與 $latex Y$ 的期望值皆為 0 ,且上述的矩陣已經是被置中了(也就是說每個 column 的數值已經扣除掉該 column 原始資料的平均值)。如果上述的變數間滿足線性模式
,
則一般最小平方法的估計結果是
。
主成份分析迴歸模型
當我們的資料矩陣 $latex \mathbf{X}$ 搜集了大量的變數,也就是 $latex p$ 很大時,在做迴歸分析時我們可能會對資料矩陣進行降維,將原本有 $latex p$ 個變數的迴歸模型轉換成只有 $latex k << p$ 個變數的迴歸模型。其中一種方式就是透過主成份分析,得到 $latex p$ 個主成份 (principal component),只留下能夠解釋最多變異的 $latex k$ 個主成份。
接著,我們來談談主成份分析的數學原理。首先,我們對資料矩陣 $latex \mathbf{X}$ 進行奇異值分解 (SVD, Singular Value Decomposition),得到以下形式:
,
如果你跟線性代數還熟悉,會知道其中
- $latex \mathbf{U}_{n \times p}= (\mathbf{u}_1, \mathbf{u}_2, \cdots, \mathbf{u}_p)$ 是資料矩陣 $latex \mathbf{X}$ 行空間 (column space) 的一組正交基底 (orthogonal basis),
- $latex \mathbf{V}_{p \times p}= (\mathbf{v}_1, \mathbf{v}_2, \cdots, \mathbf{v}_p)$ 是資料矩陣 $latex \mathbf{X}$ 列空間 (row space) 的一組正交基底 (orthogonal basis),
- $latex \mathbf{D}_{p \times p}= diag(d_1, d_2, \cdots, d_p),~d_1\geq d_2 \geq \cdots \geq d_p \geq 0$ 是一個對角矩陣,裡面的元素 $latex d_i$’s 被稱為資料矩陣 $latex \mathbf{X}$ 的奇異值 (singular value)。
主成份分析則是針對資料的共變異數矩陣 $latex \mathbf{S} = \frac{1}{n} \mathbf{X}^T \mathbf{X}$,或是說對矩陣 $latex \mathbf{X}^T \mathbf{X}$,進行特徵分解 (eigen-decomposition),特徵分解可以由資料矩陣 SVD 的結果得到:
,
其中 $latex\mathbf{V}$ 就是所謂的轉換矩陣,能夠將資料矩陣投影成主成份,而 $latex \mathbf{v}_j$’s 被稱為主成份方向 (principal component direction)。
由上述的運算,很容易得知資料的第 $latex j $個主成份以及其變異數為
,
因此每個主成份可以解釋資料的變異量其實就是其對應的奇異值,而越前面的主成分能夠解釋的變異量越多。將 SVD 的結果代入迴歸估計式中,可以得到:
。
在做迴歸分析時,假設我們想把可解釋變異量小於 $latex \lambda$的迴歸係數暴力設為 0,得到的結果會變成:
,
我們將會以這個結果與 ridge regression 的估計結果做比較,我們會很容易看出兩者間的關係。
嶺迴歸與其性質
嶺迴歸與一般最小平方法估計最大的差異,是希望能夠控制每個變數的係數大小,因此其目標函數會多加入係數大小的二次懲罰項:
,
其中 $latex lambda$ 越大,代表我們希望迴歸係數越靠近 0。將上述目標函數取一次微分求極小值,會得到
。
如果我們將資料矩陣 $latex \mathbf{X}$ 奇異值分解的結果代入,會得到:
,
跟暴力設 PC 係數為 0 的結果比較,差別在 ridge regression 將係數由 $latex \mathbf{1}_{d^2_j > \lambda}$ 轉換成平滑的 $latex \frac{d_j^2}{d_j^2+\lambda}$ 函數做收縮。
小結:PCA 與 Ridge Regression 的關係
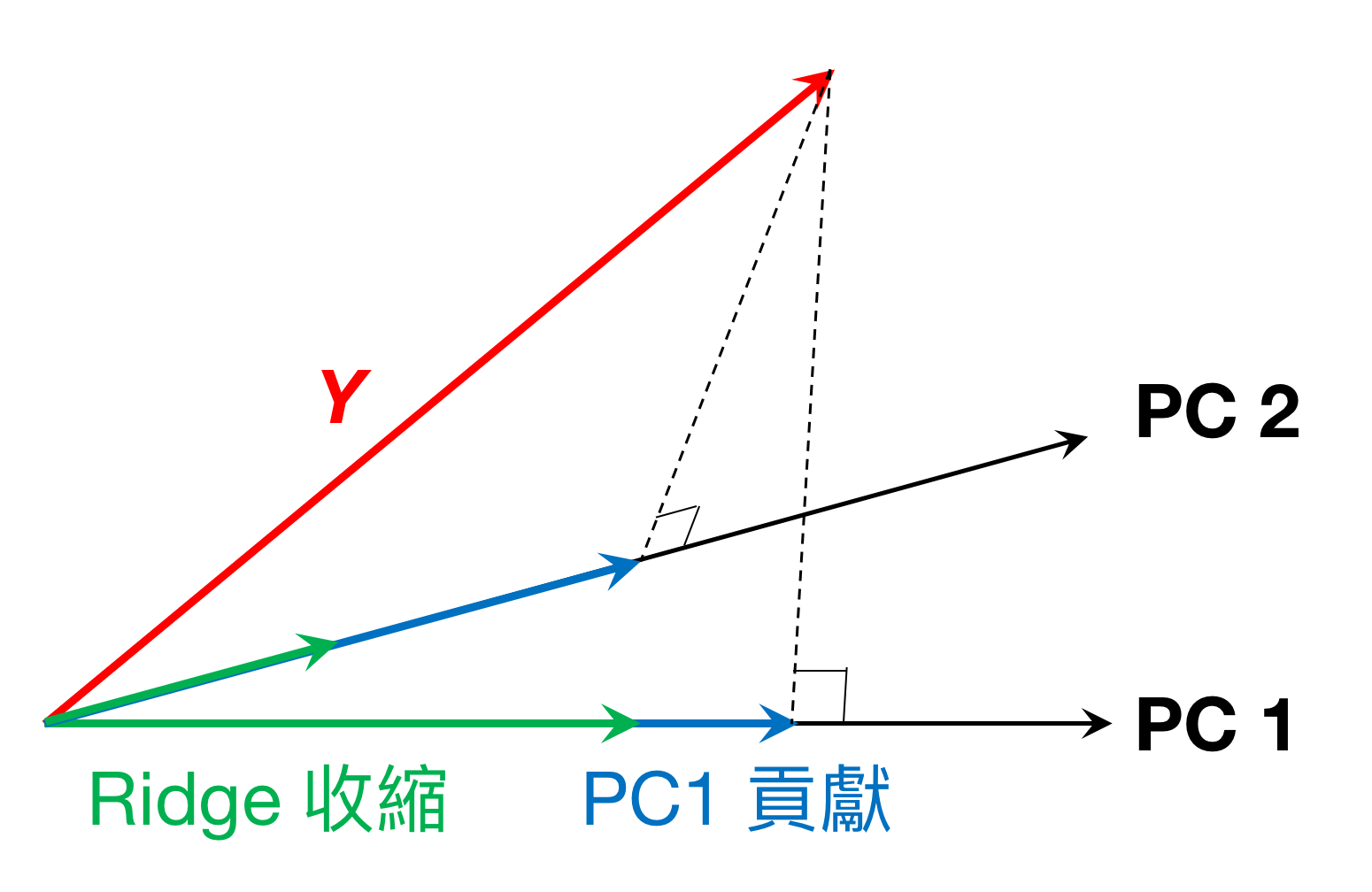
從上面的估計結果來看,越前面的 PC 獲得的權重越高(因為 $latex \frac{d_j^2}{d_j^2+\lambda}$ 為 $latex d_j^2$ 的遞增函數),而 $latex \lambda$ 越大會讓每個 PC 的貢獻越小,而且對於解釋變異較小的 PC 收縮的幅度越強。下圖是簡單的示意圖,本來我們試圖將 $latex Y$ 投影到第一個 PC 與第二個 PC 的方向上,得到的兩個投影向量 (藍色箭頭) 就是原本 PC 能夠夠獻給 $latex Y$ 的部分。而 Ridge regression 則是針對這些投影量用收縮因子 $latex \frac{d_j^2}{d_j^2+\lambda}$ 進行收縮,得到了收縮後的向量(綠色箭頭)。而且,對於第二個 PC 的收縮強度比第一個 PC 的收縮強度強。
有關 David’s Perspective 的最新文章,都會發布在大鼻的 Facebook 粉絲專頁,如果你喜歡大鼻的文章,還請您按讚或留言給我喔!

