許多領域問題除了準確的預測外,更需要了解為什麼模型會得出這樣的預測,以便辨認模型的前在風險及輔助人類做決策,因此可解釋的機器學習模型是近年機器學習發展的重要方向。在分類模型中,許多人喜歡使用變數重要性 (Variable Importance) 去解釋分類模型的判斷標準,然而對於較複雜的模型,每個變數的些微改變可能都會對預測解果有顯著影響,因此很難以變數重要性去解釋複雜的模型。有沒有什麼方法可以幫助我們解釋複雜的分類模型呢?今天跟大家介紹一個非常受歡迎的方法 – LIME (Local Interpretable Model-Agnostic Explanations) ,以「模型為什麼會將某個個體 (instance) 分類到特定類別」為核心精神,解釋複雜分類模型的判斷標準。
LIME 的命名由來
假設我們擁有一個複雜的分類模型 $latex f$,LIME 想要解決的問題是:能不能夠找到一個容易解釋的模型 $latex g$ 解釋為什麼一個個體 (instance) 會被分類到 $latex f$ 預測的類別。LIME 的名字完整說明了作者對於這個問題的核心精神─在每一個個體附近 (也就是 Local) 找出一個簡單的 / 可以被人類理解的 (也就是 Interpretable) 決策準則 $latex \xi$ (也就是 Explanation),而且對於任何的模型 $latex f$ 都能夠適用 (也就是 Model-Agnostic)。
LIME 的核心精神
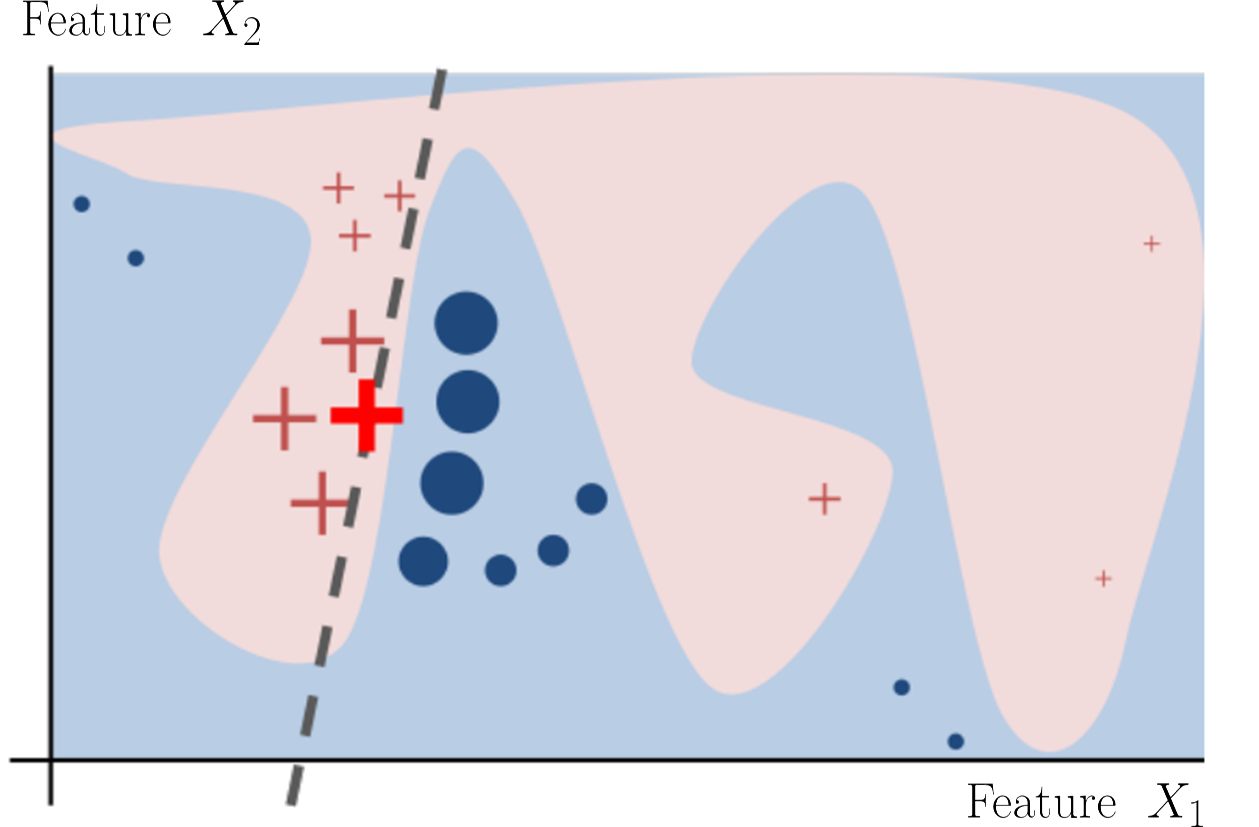
以下這張圖可以很清楚的理解上面提到的精神。假設我們希望利用特徵 $latex X_1$ 與 $latex X_2$ 去預測一個個體是 + 還是 o,一個複雜但預測準確的模型 $latex f$ 得到的決策準則如下圖紅色 / 藍色的區域。從圖中可以發現,我們很難用一個簡單的模型 $latex \xi$ (也就是可解釋的 interpretable 模型) 逼近,因此我們需要利用「局部」(local) 的特性。假設我們想要解釋下圖中較粗的 + 個體為什麼會被 $latex f$ 判斷為 + ,我們可以在該個體的附近找出一個線性的決策區域 (粗虛線),作為可解釋該個體的模型,值得注意的是,這個決策模型在該個體附近的預測準確度與 $latex f$ 相當,但在離該個體較遠的區域預測準確度就會大幅下降,這就是所謂的局部性。
我們用來估計簡單模型 $latex \xi$ 的損失函數 $latex \mathcal{L}$ 是什麼?首先,由於可解釋模型 $latex \xi$ 要用來逼近複雜模型 $latex f$ ,所以 $latex \mathcal{L}$ 與 $latex f, \xi$ 有關。此外,與 $latex \mathbf{x}_i$ 越相似的個體,應該要給予可解釋模型與複雜模型間的誤差較重權重,因此會有一個計算「與 $latex \mathbf{x}_i$ 相似與否」的核函數 (kernel function) $latex \pi_{\mathbf{x}_i}$。最後,我們希望解釋模型越簡單越好,因此也會加入模型的複雜度 $latex \Omega(g)$,其中 $latex g$是可能被選來解釋 $latex f$ 的簡單模型。總結來說,「找出可解釋模型 $latex \xi$ 解釋 $latex f(\mathbf{x}_i)$」的問題可以轉變成最佳化問題:
其中,$latex G$ 是簡單模型的家族,比如說:$latex G = \{$所有的線性分類模型$latex \} $,而任何一個 $latex g\in G$ 的模型都可以寫為 $latex g(\mathbf{X}) = \omega_0 + \omega_1 X_1 + \omega_2 X_2 $。
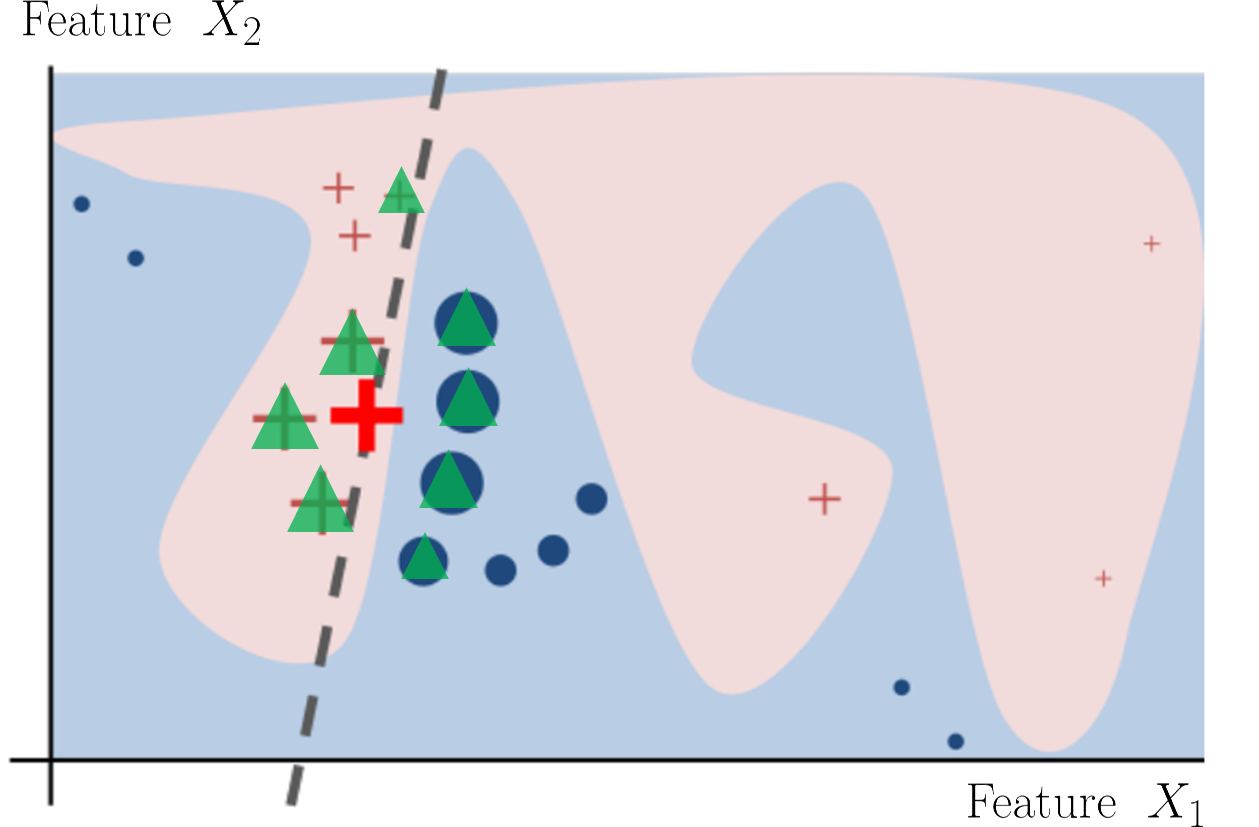
接下來的問題就是,假設給定一個個體 $latex \mathbf{x}_i$ 以及預測的類別 $latex f(\mathbf{x}_i)$,我們要用什麼資料訓練「局部的」可解釋模型 $latex g$ 呢?答案是:利用 $latex \mathbf{x}_i$ 附近的其他個體作為 $latex \xi$ 的訓練集合。以上面的例子來說,我們隨機抽出綠色的個體 (設為 $latex \mathbf{z}_1,~\cdots,~\mathbf{z}_N$),利用這些個體作為模型 $latex \xi$ 的訓練集合,試圖得到灰色虛線。
舉例而言,如果我們用來比較 $latex \mathbf{z}_1, \cdots, \mathbf{z}_N$ 與待解釋個體 $latex \mathbf{x}_i$ 相似度的函數為高斯相似度
衡量複雜模型 $latex f$ 與簡單模型 $latex g$ 間差異的函數為 $\latex \ell_2$ 損失,而衡量 $latex g$ 複雜度的方式是「非零的係數個數」,則 LIME 的問題可以寫為以下最佳化問題:
其中 $latex \lambda$ 是調整參數 (tuning parameter)。實務上,我們除了用 $latex \Omega (g)$ 來控制獲得模型的複雜度之外,更常會限制線性模型中非 0 參數的個數,以利我們進行解釋。
範例:運用 LIME 解釋癌症預測結果
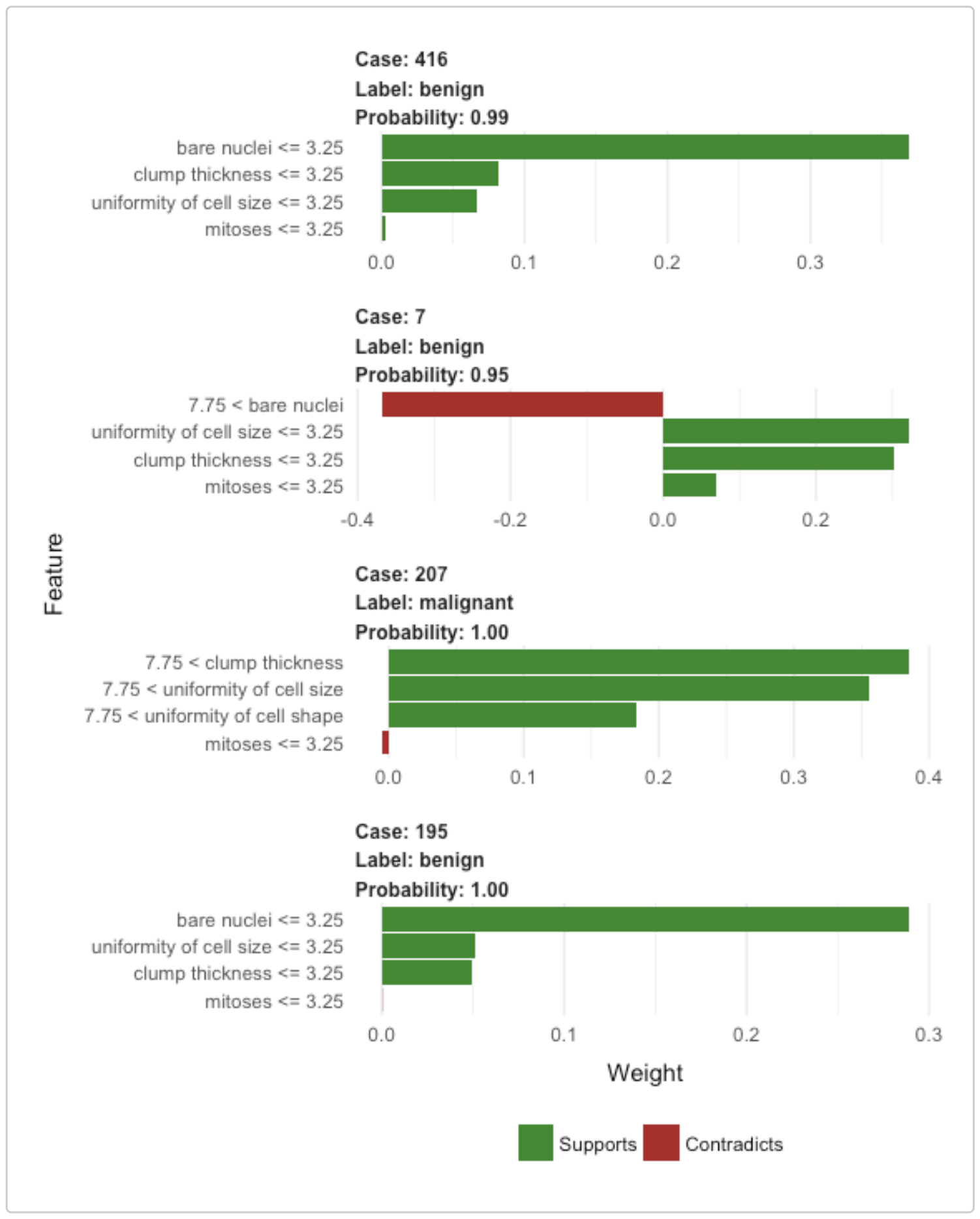
Undetstanding lime 是一個很簡單易懂的 LIME 操作教學(使用 R 的 lime 套件),裡面有一個「以腫瘤切片 (biopsy) 結果進行癌症預測」的案例,得出來的解果如下圖所示。其中每一個直方圖是一個個體,其中綠色的直條代表該特徵是支持該個體被分類到指定 label,紅色的直條代表該特徵是支持該個體被分到其他 label。預先設定線性模型中非 0 的參數不能超過 4 個,以 Case 416 為例,直方圖的 Y 軸顯示了 Case 416 得出的局部解釋模型中,4 個參數非 0 的特徵, lime 套件可以讓你選擇是否要把連續變數切成不同區間(像決策樹一樣),以便解釋複雜預測模型在 Case 416 附近的行為。
要看多少個個體,才能完整理解?
雖然只看一個個體的結果,我們對於複雜模型就有基礎的認識,但若要有全面性的理解,我們可能需要看很多個個體。但是,到底要看哪些個體呢?看多少個個體才算足夠呢?在原始的 paper 中有提供一個選擇個體的演算法,稱作 Submodular pick (SP) 演算法,但由於我沒有非常喜歡這個方法,加上這個演算法也相當直覺好懂,所以我就留給大家自己去看原始的 paper 囉 XD 有關 David’s Perspective 的最新文章,都會發布在大鼻的 Facebook 粉絲專頁,如果你喜歡大鼻的文章,還請您不吝嗇地按讚或留言給我喔!
大鼻觀點:https://www.facebook.com/davidperspective/

