邏輯迴歸通常是在學分類問題 (classification) 第一個會接觸到的模型,用來建立「二元目標變數」(Binary Output Variable) 跟解釋變數之間的關係,模型形式如下:
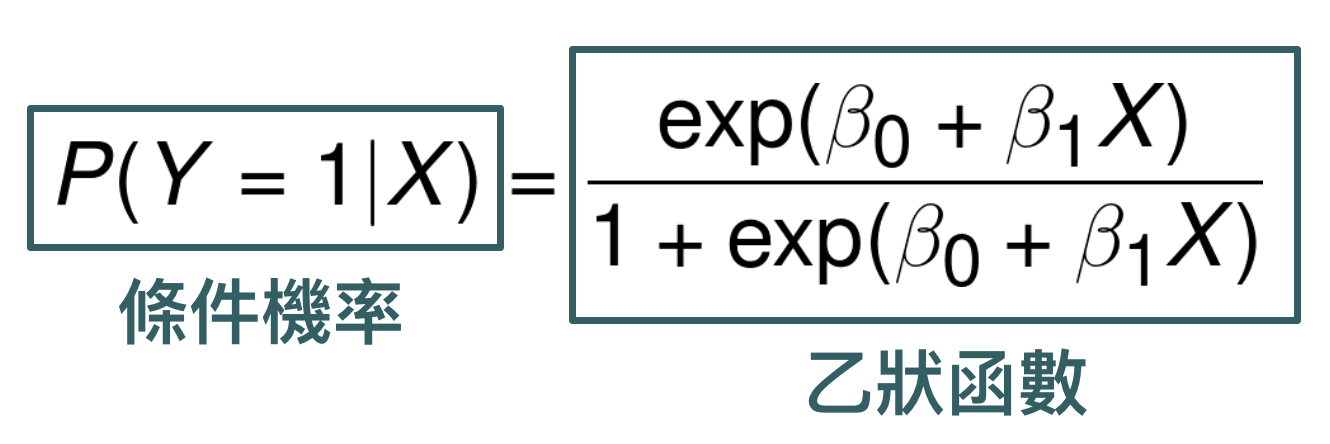
網路上其實已經有很多關於邏輯迴歸的教學文章了,所以在這篇文章中,我想要跟大家聊聊關於邏輯迴歸一些比較本質的想法。
為什麼是以機率作為建模對象?
大家應該都知道迴歸分析 (Regression) 是建立目標變數 $latex Y$ 與解釋變數 $latex X$ 間的關係,更嚴謹一點的說法是「給定一個固定的解釋變數 $latex X$,目標變數 $latex Y$ 的平均值是多少?」也就是「條件期望值 (Conditional Expectaion)」的概念:試著以線性結構去逼近 $\mathbb{E}(Y|X)$。既然屬於迴歸的一種,為什麼邏輯迴歸是「機率」為建模對象,而不是期望值呢?
其實,邏輯迴歸也是針對條件期望值進行建模的,我們知道邏輯迴歸裡面的目標變數 $latex Y$ 是一個二元變數,其中 $latex Y=1$ 的機率是 $latex \mathbb{P}(Y=1)$,$latex Y=0$ 的機率是 $latex \mathbb{P}(Y=0)$。因此可以推得條件期望值 $latex \mathbb{E}(Y|X) = 1 \cdot \mathbb{P}(Y=1|X)+ 0 \cdot \mathbb{P}(Y=0|X)=\mathbb{P}(Y=1|X)$。也就是說,其實邏輯迴歸還是建立目標變數 $latex Y$ 的平均值與解釋變數 $latex X$ 間的關係,只是 $latex Y$ 的平均值剛好跟 $latex Y = 1$ 的機率是一樣的。
為什麼是乙狀函數 (Sigmoid Function) ?
以前大鼻在學邏輯迴歸 (Logistic Regression) 時,一直有一個很大的疑惑:到底為什麼會跑出來乙狀函數 (Sigmoid Function) 這個東西呢?以前課本上大概會說,因為乙狀函數是落在 (0,1) 之間,符合邏輯迴歸針對機率建模的特性,而且可以微分,但我最大的疑問是:那為什麼不選 $latex sin^2 x$ 呢?為什麼偏偏就是乙狀函數呢?(乙狀函數的形式如下圖所示。)
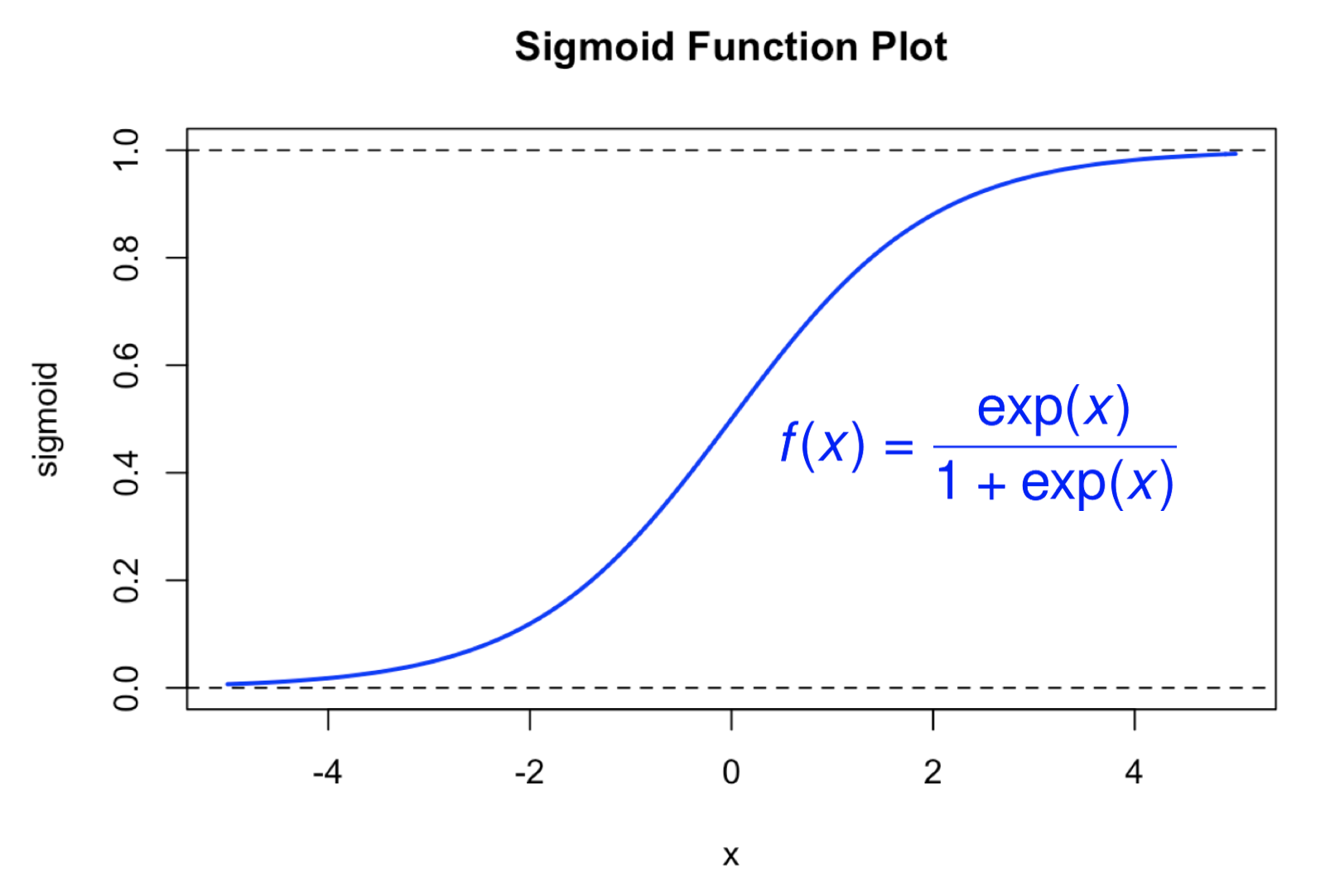
假設我們現在想要分析的問題是:一個人在買早餐時會不會順便買一杯大冰奶?要不要買大冰奶的影響因素有很多,比如說:今天有重要的會議要開, 千萬不能落屎,就不買;昨天算命阿姨說喝一杯搭冰奶就可以找到女朋友(請見阿翰Po影片),那當然是要買;這個月已經沒有預算可以喝小確幸大冰奶,不買。可能的原因有三個,但我們先專注於「早餐預算」($latex X$) 與「是不是買大冰奶」($latex Y$) 之間的關係,把他畫成以下散布圖,並建立 $latex Y = \beta_0 + \beta_1 X$的迴歸模型,會發現結果非常差。
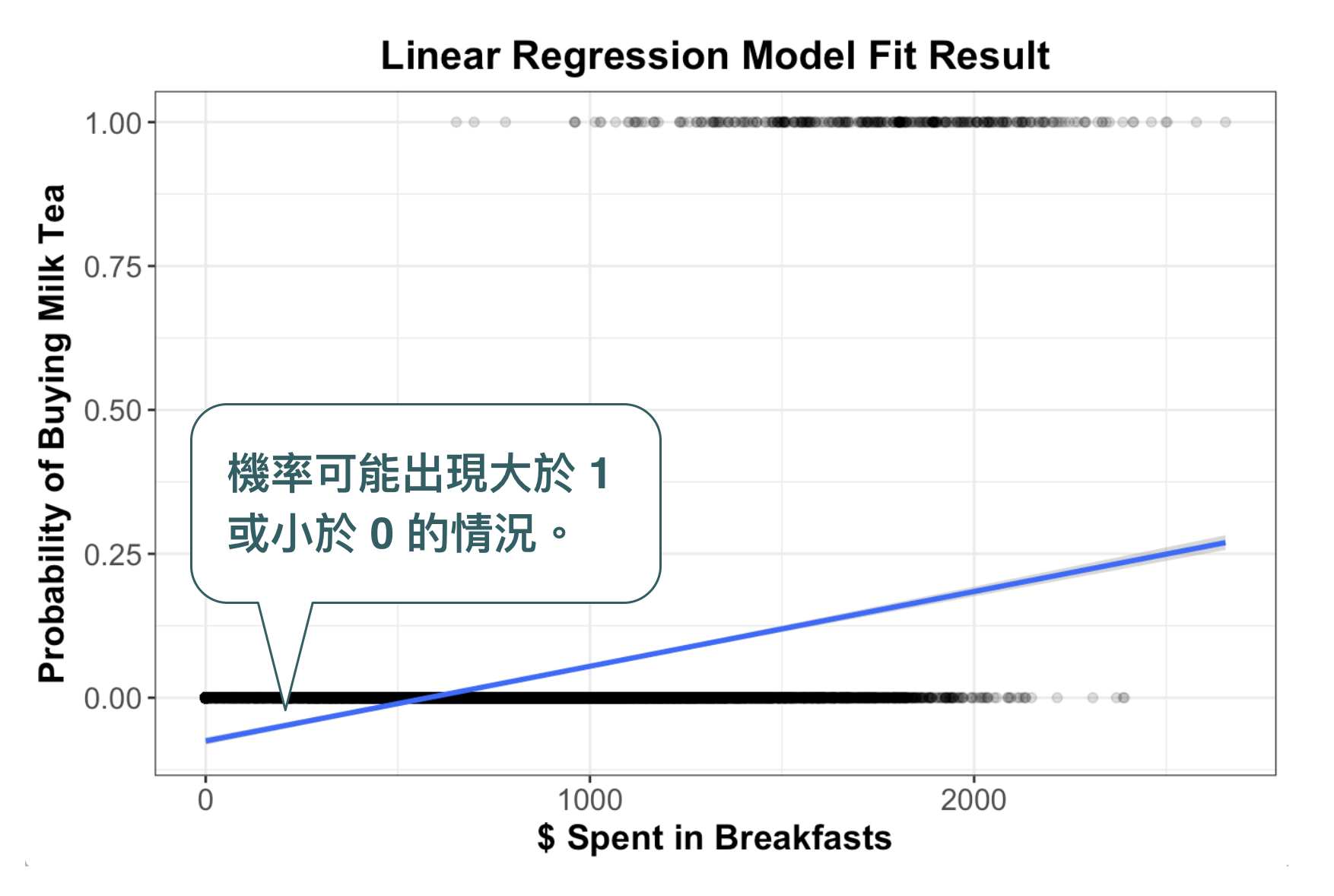
但仔細看圖,仔細看喔,是不是好像是一個乙字呢?我們如果真的拿乙字來做建模,結果如下所示。可以發現,「早餐預算越高」購買大冰奶的機率越大,但中間有一些區段(機率上升段)剛好是只靠預算沒辦法完全捕捉的區段,這樣做是不是很符合現實情況呢?所以,真要說為什麼會選用乙狀函數?大鼻是沒有考究為什麼,但我自己說服自己的方法是,「用眼睛看」就覺得很合理 XD
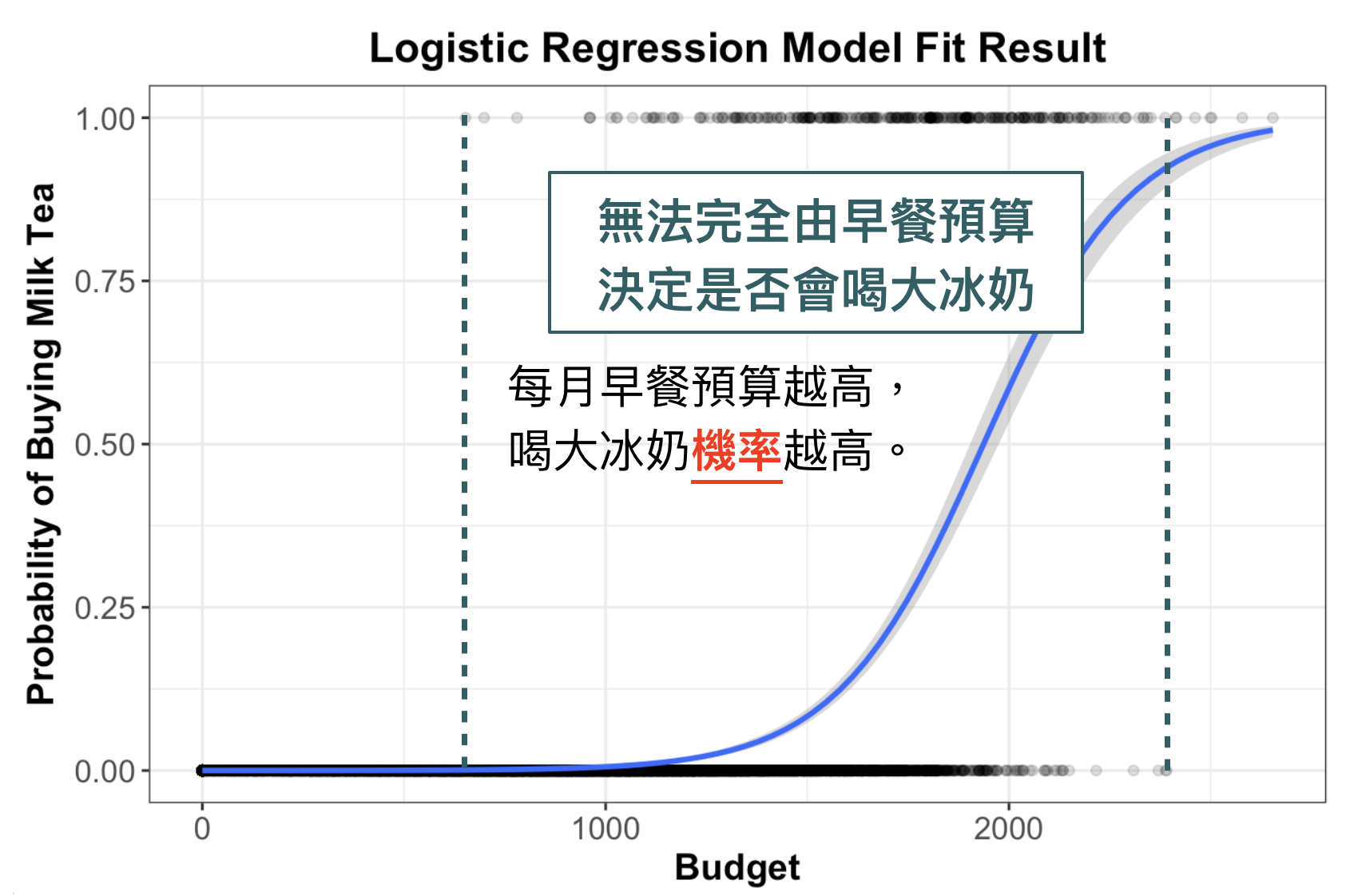
為什麼要用最大概似法 (Maximum Likelihood Estimation)?
有些剛碰機器學習的人,可能只知道用 R 或 Python 可以估計出參數,但到底這個參數是怎麼估的可能沒有很清楚。在迴歸分析中,我們是使用最小平方法 (Ordinary Least Square Estimation) 估計參數,相信大家高中數學其實有學過。那為什麼邏輯迴歸不能用最小平方法呢?
有人說,因為邏輯迴歸不是線性的,這個說法是不對的!因為我們可以把邏輯回歸的模型轉成線性的形式如下:

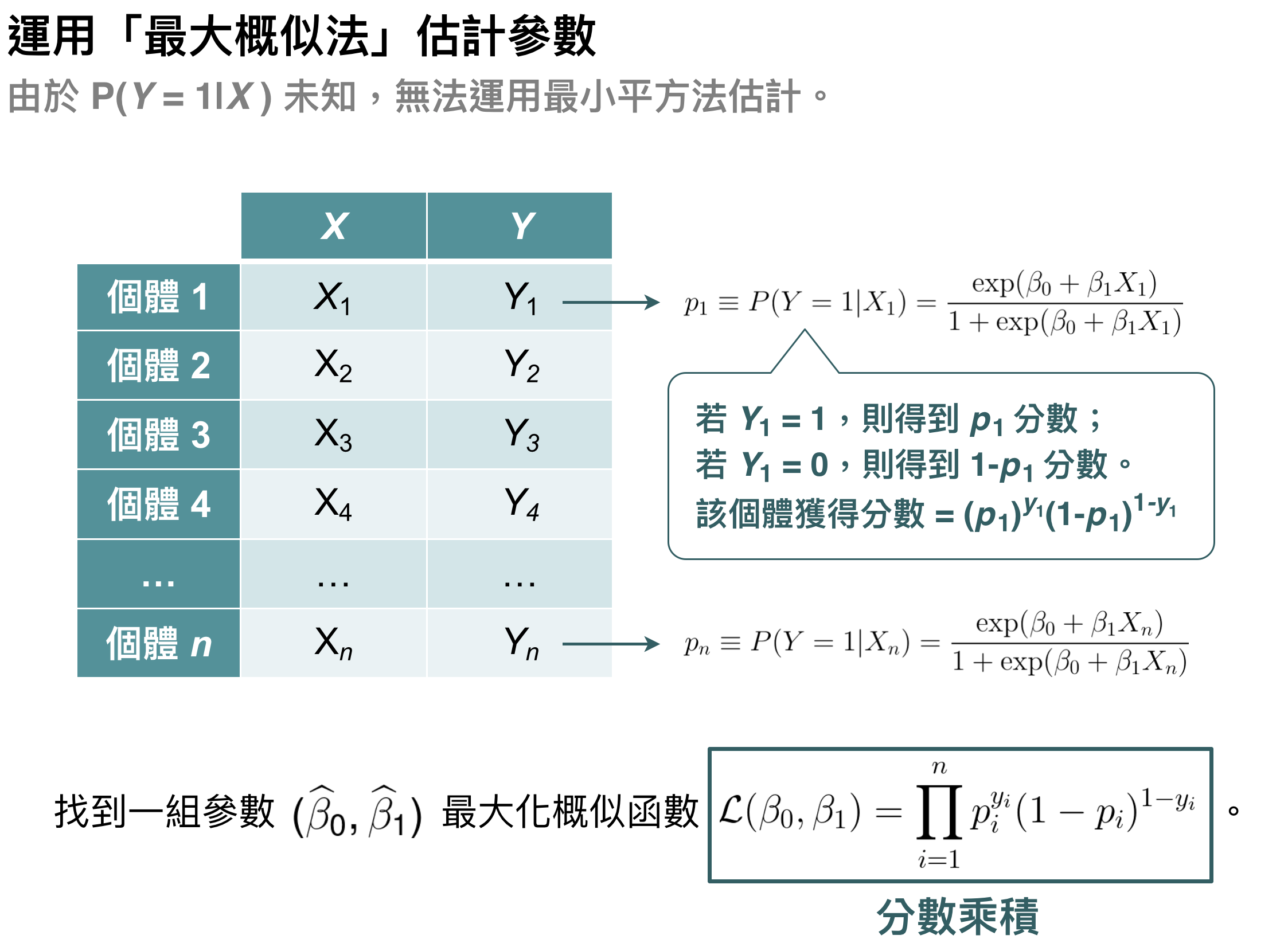
主要原因很簡單,因為迴歸分析中 $latex Y$ 是已經觀察到的資料,可是邏輯迴歸中 $latex P(Y=1|X)$ 是資料裡面無法觀察到的,所以我們就沒辦法用傳統的最小平方法估計,而要採用最大概似法 (Maximum Likelihood Estimation)。至於最大概似法的原理是什麼,可以用下面這張圖很清楚的解釋。
除了交叉驗證 (Cross Validation) 之外,有哪些選模指標?
其實邏輯迴歸除了用交叉驗證比較分類準確性、AUC等等指標之外,還有一些很好用、有理論基礎的量化指標可以選取,像是 Pseudo R-Square、Information Criteria 等,常見的選模指標裡列在下表:

小結:在學一個模型時,記得問why?
邏輯迴歸是一個非常經典而常見的模型,但我一直覺得大部分網路上的教材沒有把他的本質講得很清楚。其實,有些直覺但是在許多進階模型都會使用的想法,是要從最簡單的模型開始思考的。因此,下一次在學習一個常見的模型時,不妨多問問 why?當你了解為什麼要這樣設計後,很多更複雜的模型反而會變得很直覺而簡單喔!
有關 David’s Perspective 的最新文章,都會發布在大鼻的 Facebook 粉絲專頁,如果你喜歡大鼻的文章,還請您不吝嗇地按讚或留言給我喔!


哈囉,最近參加一個比賽,主要是藉由一些產品上senser過去的歷史資料來預測產品品質,有想到用邏輯迴歸,可是用的時候發現他是會將好的機率及不好的機率列出來,並不是輸出品質,想問一下邏輯迴歸只能當作解決二分類的問題嗎?謝謝
邏輯迴歸也有 multi-class 的版本,可以 google 看看喔~資料很多!