Kaggle 的過度配適與完美預測─淺談自適性資料分析

David Huang
%e8%a1%a8%e6%a0%bc123

許多的醫學、環境、社會學研究、甚至是網路軟體公司都大量運用「假設檢定」的統計架構進行分析，假設檢定的概念大家可以看看「P-值已經死了嗎？莫須有罪名的最大受害者！」這篇文章。在這樣的統計架構下，通常我們會根據該領域的問題去蒐集一組「隨機樣本」  (random sample)，並根據隨機樣本去推論整個母體 (population) 的性質。在科學研究中，因為假設檢定試著控制的便是型一錯誤(Type I Error) 的機率，因此在統計方法被誤用的情況下，時常會造成型一錯誤/False Discovery的發生。

然而，其實 False Discovery 發生的原因，也可能是資料分析的自適性天性 (adaptive nature)。「自適性」指的是「在我們選擇最終的統計模型時，時常會建立在過去與資料互動的經驗」，比如說：在進行一連串統計分析時使用了有重疊的資料集合，再進行統計建模時先進行資料預處理 (如：特徵選取)，重複使用保留的測試集合 (holdout testing set)等。在自適性資料分析的情況下，我們最常犯的錯便是過度配適 (overfitting)，造成資料分析的結果與實際情況不吻合。

 

自適性資料分析 (Adaptive Data Analysis) 的討論從 2015 年便開始發展，除了分析在「自適性資料分析的架構下」是否能夠找到一組機制 (mechanism) 使得分析結果與真實母體的性質外，如何找出有效的演算法，透過設計「查詢」(query) 演算法，更快逼近真實母體的性質。

 

自適性問題的常見案例：機器學習線上比賽

 

自適性資料分析最典型的案例，就是 Kaggle 的比賽機制：

  • 比賽者會擁有一組 training set，可以用來訓練比賽者的模型。
  • 比賽者同時會擁有一組測試集合 (testing set)，這組集合是固定的，當比賽者上傳自己訓練模型在測試集合上的預測結果，會得到該模型在測試集合上的分數 (score)。

因此，我們可以透過一些手法，透過大量上傳不同模型的方式去做參數調整 (parameter tuning)。當然現在的比賽只會將一部份測試集合得到的分數呈現在公開記分板上，另一部份的結果會在總成績結算時才公告，而會有這樣的設計，主要原因就是因為這樣得出的結果時常會過度配適該組固定的測試集合 (testing set)。

 

 

自適性資料分析的數理模型

 

在自適性資料分析中，通常會有以下的假設：

  • 樣本的砥柱集合為 (support) \mathcal{X}。
  • 我們可以蒐集隨機樣本  \mathbf{x} = (x_1,\cdots,x_n) \in \mathcal{X}^n，其母體分配為 \mathcal{P}。
  • 分析師 \mathcal{A} 希望能夠透過一連串 k 次的查詢 (q_1, \cdots, q_k) \in Q^k 去逼近真實的母體性值，其中 Q 蒐集了所有可能的查詢方法。
  • 這些查詢背後的機制 \mathcal{M} 很簡單：給於一組隨機樣本 \mathbf{x} 與一次查詢 q_j，該機制 \mathcal{M}(\mathbf{x}, q_j) 會根據這次的樣本與查詢給予答案 a_j。
  • 真正的母體性值記為 q_j(\mathcal{P}) =  \mathbb{E}_{X\sim \mathcal{P}} (q_j (X))。

 

自適性資料分析最大的特色，就是每一次的查詢 q_j 與答案 a_j，都與前一次的 q_{j-1} 與a_{j-1}存在統計關聯性 (statistical dependency)，這種關聯性很容易讓我們去過度配適被用來作為查詢的資料集合，像是這篇部落格文章：Competing in a data science contest without reading the data就有用一個簡單的例子說明為什麼過度配適 public board 的資料在 Kaggle 比賽中會發生。在這種情境下，一個很自然的疑問是，「有沒有足夠好的機制 \mathcal{M}，讓我們在查詢中不要過度配適？」

 

圖片1

 

 

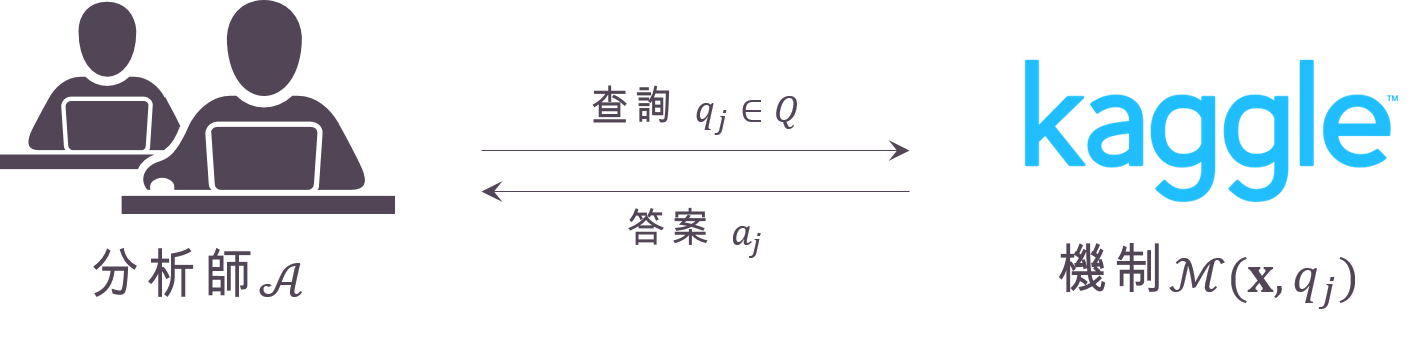
查詢的種類：統計查詢、 \Delta-敏感查詢與最小化查詢

 

在前面的討論中，我們還沒有談到「查詢」的方法。查詢一般來說可以分成三種主要的類型：一是「統計查詢」(Statistical Query)，二是「\Delta-敏感查詢」(\Delta-sensitive Query)，三是「最小化查詢」 (Minimization Query)。

 

在「統計查詢」的家族中，令 q:\mathcal{X}\rightarrow [0,1] 是一個定義在砥柱集合上的函數，一個統計查詢由以下兩個要素組成：

  • 真實待估計的母體性值為 q(\mathcal{P})=\mathbb{E}_{X\sim \mathcal{P}} (q (X))。
  • 分析師使用動差估計式 q(\mathbf{x})=\frac{1}{n} \sum\limits_{i=1}^n q(x_i)。

其中，該次查詢的答案 a 與母體的誤差為 err^{\mathcal{P}}(q, a) = a - q(\mathcal{P})，答案 a 與樣本的誤差為 err(q, a) = a - q(\mathbf{x})。

 

第二種常見的查詢叫做 \Delta-敏感查詢。假設有兩組樣本 \mathbf{x} 與 \mathbf{x}'，他們兩者 有 n-1 個相同的元素，只有一個元素是不同的，這兩個樣本的關係我們用 \mathbf{x}\sim\mathbf{x}'表示。所謂的「敏感性」(sensitivity) 分析指的是這樣的兩組樣本對查詢結果會帶來何種影響。在「\Delta-敏感查詢」的家族中，令 q:\mathcal{X}\rightarrow \mathbb{R} 是一個定義在砥柱集合上的函數，而且滿足「如果樣本中只有一個元素不同，則查詢結果不會差距太大」，也就是對於任何 \mathbf{x}\sim\mathbf{x}'，|q(\mathbf{x})-q(\mathbf{x}')|\leq \Delta，其中 0\leq \Delta \leq 1。如果 \Delta = O(1/n)，則該查詢稱為「低敏感性查詢」(low-sensitivity query)，此時 \Delta-敏感查詢 其實也是一種統計查詢。

 

「最小化查詢」是\Delta-敏感查詢的推廣，假設 \mathcal{L}:\mathcal{X}\times \Theta \rightarrow \mathbb{R} 是一個損失函數，其中 \Theta 是參數空間。一個最小化查詢希望「如果樣本中只有一個元素不同，則查詢結果在損失函數的角度下不會差距太大」，也就是 \sup\limits_{\theta\in\Theta, \mathbf{x}\sim\mathbf{x}'} \left| \mathcal{L}(\mathbf{x},\theta) - \mathcal{L}(\mathbf{x}',\theta)\right| \leq \Delta。此時，誤差的定義將變為：

  • 母體的誤差：err^{\mathcal{P}}(\mathcal{L}, \theta) =\mathbb{E}_{X\sim \mathcal{P}} \mathcal{L}(X,\theta) -\mathbb{E}_{X\sim \mathcal{P}} \min_{\theta'} \mathcal{L}(\mathbf{x},\theta') 。
  •  樣本的估計誤差：err(\mathcal{L}, \theta) = \mathcal{L}(\mathbf{x},\theta) - \min_{\theta'} \mathcal{L}(\mathbf{x},\theta')。

 

查詢的準確性 (Accuracy)

 

由於在自適性資料分析中，我們希望能夠設計出一組足夠好的機制 \mathcal{M}，因此我們在此先定義什麼叫「足夠好」。一個足夠好的查詢機制要滿足兩個條件，一個叫做「準確性」(Accuracy)，一個叫做「恆定性」(Stability)。

首先，我們先介紹準確性。如果一個查詢機制 \mathcal{M}滿足 \mathbb{P}_{\mathbf{x}\in\mathcal{X},q_j\in Q}\left(\max\limits_{j=1,\cdots,k}|err(q_j(\mathbf{x}) - a_j|) > \alpha\right) < \beta，我們就稱其具有 (\alpha,\beta) -樣本準確性 ((\alpha,\beta) -sample accuracy)。也就是說，我們希望每一次分析師自行估計的查詢值 q_j(\mathbf{x}) ，與該次查詢的真實答案 a_j ，兩者的誤差超過\alpha的機率被 \beta 控制住。同理，我們可以定義(\alpha,\beta) -母體準確性 ((\alpha,\beta) -population accuracy)： \mathbb{P}_{q_j\in Q}\left(\max\limits_{j=1,\cdots,k}|err^{\mathcal{P}}(q_j(\mathbf{x}) - a_j|) > \alpha\right) < \beta

 

差分隱私 (Differential Privacy)

 

接下來，我們要介紹很特別的穩定性，叫做 max-KL-stability，其中 KL 就是我們常用來計算兩個機率分配距離的 KL Divergence (抱歉大鼻不知道如何準確的翻譯成中文)。其實 max-KL-stability 跟一個密碼學中的概念是一樣的，這個概念叫做「差分隱私」(Differential Privacy)。

 

其實差分隱私這個概念在你我手中的 iphone 手機中都有被運用到，蘋果是世界上最重視使用者隱私的公司之一，因此他在蒐集使用者體驗的方法便是使用差分隱私的方式蒐集資料。這一篇報導有試著用比較簡單的話說明差分隱私的意涵。

 

appleprivacy5

(Apple 在 2016 年的WWDC 上提到其蒐集客戶使用行為的方式是利用具備差分隱私性質的演算法)

 

什麼樣的演算法具備差分隱私性呢？設 \mathcal{W}: \mathcal{X}^n \rightarrow \mathbb{R} 為一隨機演算法，R \subset \mathbb{R} 是實數軸上的任意一個子集合，\mathbf{x}\sim\mathbf{x}'為認兩組只有一個元素不同的樣本，如果 \mathcal{W} 是一個具備(\epsilon,\delta)-差分隱私性的演算法，則 \mathbb{P}(\mathcal{W}(\mathbf{x})\in R)\leq e^\epsilon \cdot \mathbb{P}(\mathcal{W}(\mathbf{x}')\in R) + \delta)。

 

直覺上來說，差分隱私的概念是：一個隨機演算法如果作用在兩個差距不大的資料集合上，該演算法得到的結果有很高的機率不會差太多。因此，蘋果的做法是在蒐集資料的時候，可以在資料裡面加入微量的隨機誤差，這樣就不會完全洩漏個人資料，同時，因為演算法具備差分隱私性，所以跟直接蒐集真實個人資料的結果不會差太多。從這裡也可以看出來差分隱私跟查詢的關聯─一個查詢演算法如果具備差分隱私性，代表每一次查詢的結果不會有太大的差距。

 

差分隱私 (Differential Privacy) 與自適性資料分析

 

我們可以把整個自適性學習的體系想像成一個隨機演算法 \mathcal{W}_{n,k,Q}[\mathcal{M},\mathcal{A}]: \mathcal{X}^n \rightarrow (Q\times \mathbb{R})^k，情中該隨機演算法的輸入為一組樣本\mathbf{x}，輸出則是連續 k 次的查詢與結果 \{(q_1,a_1),\cdots, (q_k,a_k)\}，其中每一次分析師選取的 q_j 都會與前一次的答案 a_{j-1} 有關。

 

那麼怎麼樣的查詢機制叫做具備差分隱私性\mathcal{M}呢？在這裡 recap 一下，分析師 / 建議者 (adversary) 在機器學習領域是很出現的術語，指的其實就是機器學習中的 hypothesis set (比如說 SVM 的 hypothesis set)，而查詢家族 Q 則是你查詢技巧的限制範圍。一個具備(\epsilon,\delta)-差分隱私性的機制  \mathcal{M} 代表對於任何的分析師，在一個給定的查詢家族內，(q_1,\cdots,q_k) 與答案 (a_1,\cdots,a_k) 都不會差太多，也就是說：對於任何的分析師\mathcal{A}，演算法 \mathcal{W}_{n,k,Q}[\mathcal{M},\mathcal{A}] 都具備(\epsilon,\delta)-差分隱私性。

 

Kaggle 是完美預測還是過度配適？

 

最後，我們終於可以談到今天想要說的主要主題：在 Kaggle 比賽上得到第一名的模型，到底是過度配適 Kaggle 的測試集合，還是真正能夠完美預測母體的性值呢？接下來要跟大家介紹一個主要轉移定理：儘管我們透過上傳測試結果查詢了很多次，我們在該測試集合上得到的樣本準確性，是可以推廣到母體準確性的─只要我們的機制具備差分隱私性。該定理如下：

 

令 Q 為一個 \Delta-敏感查詢的家族，對於 \alpha, \beta \in (0, 0.1)，若機制 \mathcal{M} 具備：

  1. \left(\frac{\alpha}{64\Delta n},\frac{\alpha\beta}{32\delta n}\right)-差分隱私性，且
  2. \left(\frac{\alpha}{8},\frac{\alpha\beta}{16\Delta n}\right)-樣本準確性，

則該機制就會具備 (\alpha, \beta)-母體準確性。也就是說，只要我們的查詢機制足夠精妙(具備差分隱私性)，我們其實是可以將查詢機制的準確性推廣到母體精確性。

 

在最後的結尾，又要再提一次(我記得好像講過幾百次XD)，大數據時代，樣本跟母體的差別還是非常重要的！！不論是機器學習的理論，到這篇文章探討的自適性資料分析，其實都是在討論「到底在樣本觀察的現象能不能推廣到母體」，樣本數很大的時候，代表的其實是「樣本跟母體的誤差」已經克服收斂速度的問題，不是所謂的「樣本即母體」！

 

有關 David’s Perspective 的最新文章，都會發布在大鼻的 Facebook 粉絲專頁，如果你喜歡大鼻的文章，還請您不吝嗇地按讚或留言給我喔！

大鼻觀點：https://www.facebook.com/davidperspective/

About David Huang

目前在台灣大學就讀統計碩士學位學程。我的研究領域是特徵表達與降維分析、序列決策模型、以及財務時間序列，我喜歡用商業的觀點切入大數據與資料科學！

發表迴響

你的電子郵件位址並不會被公開。 必要欄位標記為 *