譜分群 (Spectral Clustering) ─ 運用圖論 (Graph Theory) 進行分群

分群 (Clustering) 是非監督式學習 (Unsupervised Learning) 中很重要的主題，目標是把「相似的個體 (individual) 通過演算法把相似的個體分到同一個子集合 (subset)」。比如說，Spotify 有許多不同類型的歌曲，可以透過語言、風格、歌手等相關資訊，將「相似」的歌曲分在一群；Netflix 有眾多使用者，可以透過他們過去的觀看影集，將偏好相似的使用者分在一群。

網路上有許多分群演算法的教學，如：K-means Algorithm、Hierarchical Clustering等，但好像比較少有人談到譜分群 (Spectral Clustering) 這一大類非常重要的分群演算法，因此我想跟大家分享一下。

分群的基本精神

假設現在有一組資料集合 $latex \mathcal{D} =\left\{\mathbf{x}_1,\cdots,\mathbf{x}_n\right\}$ 是 $latex n$ 個個體 (individual) 的特徵向量 (feature vector)，其中 $latex \mathbf{x}_{i} \in \mathbb{R}^d$ 是一個 $latex d$ 維度的向量。

在聚類分析中，我們希望找到一個資料集合 $latex \mathcal{D}$ 的分割 (partition) $latex \Delta = \left\{C_1,\cdots,C_K\right\}$，其中 $latex C_{i}\neq \phi$ 代表的是一個群集 (cluster) ，也就是：$latex \cup_{i=1}^K C_i = \mathcal{D}$ 且 $latex C_i  \cap  C_j = \phi$，使得目標損失函數 $latex \mathcal{L}(\Delta)$ 極小化。

緊緻性 vs. 連通性 ─ 聚類分析的兩難

在設計分群演算法時，最難回答的問題便是「什麼樣的個體該被分在一起」，一般來說，我們會又兩種角度思考這個問題─一是緊緻性 (Compactness)，二是連通性 (Connectedness)，這是點集拓樸 (Point-set Topology) 中常被討論的兩個性質，在做分群演算法時我們也會以這兩種性質去進行分群。

以緊緻性的角度出發，我們會希望建構出的集群 (cluster) 是緊緻的，因此會傾向把「距離 (distance) 必較靠近的幾個資料點」分在同一群。如果是以連通性的角度出發，通常會傾向把「可以被串接在一起的資料點」分在同一群。

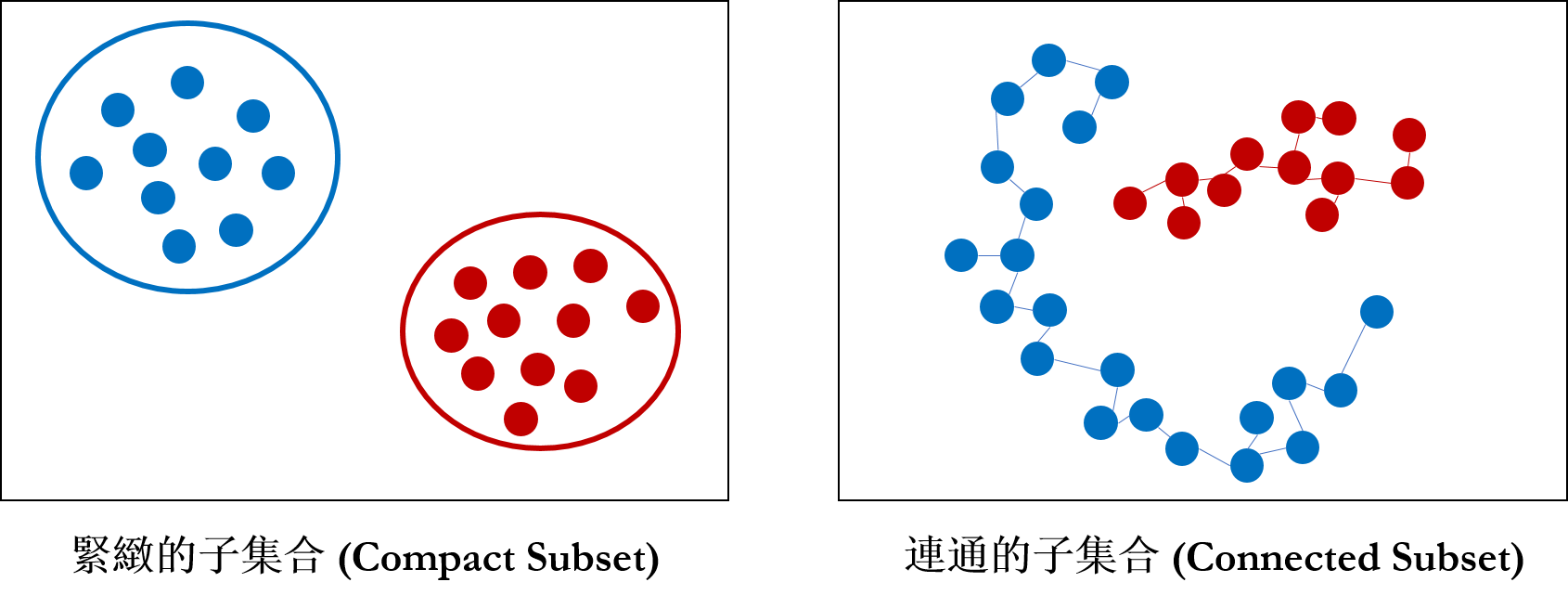
如果只從資料點 (data point) 與距離的角度來看，最大的問題在於資料的「形狀」(Shape)考慮進去，因此拓樸資料分析 (Topological Data Analysis)便是利用「形狀」特徵 (feature) 去捕捉連通性的特殊方法。

拓樸資料分析是近 10 年來才開始興起的新方法，但處理「連通性」的分群演算法找在2000年初就已經發展成熟了。當初在進行連通性建模時，很直覺的想法是引進圖論 (Graph Theory) 的分析架構進行處理，同時利用「距離」的資訊建立資料點的圖 (Graph)，因此在介紹 Spectral Clustering 的時候，一定要先從基本的圖論開始介紹。

相似圖 (Similarity Graph) 的建立

考慮我們的資料集合 $latex \mathcal{D} =\left\{\mathbf{x}_1,\cdots,\mathbf{x}_n\right\}$，我們可以透過資料點 $latex i$ 與資料點 $latex j$ 的距離建立資料點 $latex i$ 與資料點 $latex j$ 的「相似性」(Similarity) $latex s_{ij}$，比如說： 高斯核相似函數 (Gaussian Kernerl Simlarity) $latex s_{ij} = 2\exp\left(\frac{-\|\mathbf{x}_i – \mathbf{x}_j\|^2_2}{2\sigma^2}\right)$，其中 $latex \|\cdot\|_2$ 是兩點之間的歐式距離 (Eucledian Distance)。

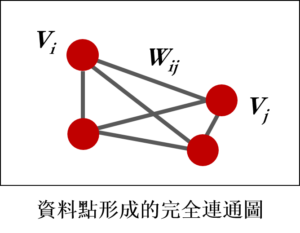
一個權重圖 (Weighted Graph) $latex G=(V,E)$ 由節點 (vertex) $latex V$ 與邊 (edge) $latex E$ 構成。我們可以將資料點 $latex \mathbf{x}_i $ 視為相似圖上的節點 $latex v_i$，而兩個節點 $latex v_i$ 與 $latex v_j$ 的邊上會攜帶著權重  (weight) $latex w_{ij}$，如果權重$latex w_{ij} = 0$，代表兩個節點不是連通的 (unconnected)，權重越大則代表連結性越強，因此我們可以用 高斯核相似函數代表兩個節點的權重。節點 $latex v_i$ 的分支度 (degree) 定義為 $latex d_i = \sum_j  w_{ij}$，也就是與其他節點間權重的加總。我們定義權重矩陣 $latex W = [w_{ij} ] $，分支度矩陣為 $latex D = diag(d_1,\cdots,d_n)$。

通常資料點形成的圖會是無方向圖 (Undirected Graph)，也就是 $latex w_{ij}=w_{ji}$，對於所有$latex i,j = 1,\cdots,n$，因此 $latex W$ 矩陣會是一個對稱矩陣。此外，資料點利用高斯核相似度函數建立出來的圖會是一個完全連結圖 (Fully Connected Graph)，也就是說對於 $latex \mathbf{x}_{i} \neq \mathbf{x}_{j}$，兩點間的權重$latex w_{ij} \neq 0$，代表任兩點之間都有被連結在一起。而 Spectral Clustering 的目標就是試著把這張完全連結圖斷開連結(燒!燒!)，切割成不同的集群。

對於一個節點的子集合 $latex A\subset V$，有兩種方法定義集合 $latex A$ 的大小，其一是 $latex |A|=$ 該節點所有的邊數，二是 $latex vol(A) = \sum_{i\in A} d_i$。任兩個不相交集合 $latex A,B$ 之間的權重定義為 $latex W(A,B) = \sum_{i\in A, j \in B}w_{ij}$。

 Graph Laplacian 矩陣

假設無方向性加權圖 $latex G$ 有一個分割 $latex \Delta = \left\{C_1,\cdots,C_K\right\}$，我們可以透過Laplacian Embedding 的方式，找出分割 $latex \Delta $。Ng, Jordan, and Weiss (2002) 的論文中使用標準化的 Graph Laplacian 矩陣進行分割，該矩陣的定義為：

$latex \mathcal{L}_{sys} = I – D^{-1/2} W D^{-1/2}$，

由一些簡單的數學推導，我們可以知道：

1. 對於任意一個向量 $latex f \in \mathbb{R}^n$， $latex f^T \mathcal{L}_{sys}f = \frac{1}{2}\sum_{i,j=1}^n w_{ij}\left( \frac{f_i}{\sqrt{d_i}}-\frac{f_j}{\sqrt{d_j}}\right)^2$。
2. $latex \mathcal{L}_{sys}$ 是一個半正定 (positive semi-definite) 的矩陣，且其有 $latex n$ 個非負的特徵值 (eigen-value)。

 圖的分割、Graph PCA與譜分群

根據以下定理，我們可以得知 $latex \mathcal{L}_{sys}$ 可以幫助我們得到我們想要的集群：

假設$latex G$是一個無方向性、正權重的加權圖 ，則若 $latex \mathcal{L}_{sys}$ 有 $latex K$ 個特徵值的解為 0，則存在分割  $latex \Delta = \left\{C_1,\cdots,C_K\right\}$，其中$latex C_i$ 都是完全連通的。此外，特徵值為 0 的特徵空間是由 $latex D^{1/2}\mathbb{1}_{C_i}$ 所張成。

因此我們可以知道，只要把 Graph Laplacian 的矩陣做譜分解 (Spectral Decomposition) ，找出前 $latex K$ 個最小的特徵值與對應的特徵向量，將原本的資料點投影到這 $latex K$ 個特徵向量上，再將投影的結果進行 $latex K$-means clustering，就可以找出原本每個集群都是完全連通的分割！在這裡說個題外話，其實這個步驟很像是在對圖做 PCA再做分群，只是圖的共變異數矩陣是用 Graph Laplacian 矩陣，以及現在尋找的是最小的特徵值。

因此，Ng, Jordan, and Weiss (2002)  提出的譜分群演算法如下，取自 Luxburg (2007)：

 小節：運用圖論進行連通性建模的譜分群

大家看到這裡可能已經被數學搞昏頭了，大鼻想跟大家分享的是，其實機器學習是一個很特別的領域─運用大量數學理論套用到實際資料中，可以做出不錯的結果，像是 3D 成像的分群用譜分群坐騎時表現會特別好喔！

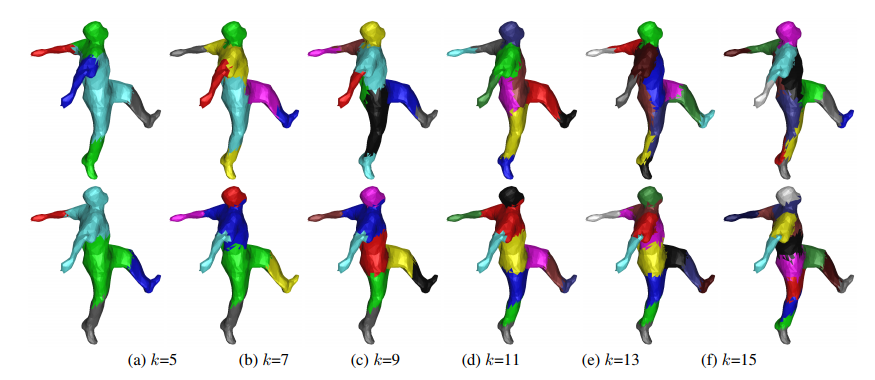
另外，雖然這邊沒有提到未標準化的 Graph Laplacian 矩陣，但標準化與未標準化的差別，其實就跟相關係數矩陣與共變異數矩陣之間的差別一樣，Laplacian embedding 其實跟 PCA 也是有 87% 像，在機器學習的領域中，其實很多理論都可以被串在一起的！

最後，如果你對文章中提到的paper有興趣，請看：

1. Ng, A. Y., Jordan, M. I., & Weiss, Y. (2002). On spectral clustering: Analysis and an algorithm. In Advances in neural information processing systems (pp. 849-856).
2. Von Luxburg, U. (2007). A tutorial on spectral clustering. Statistics and computing, 17(4), 395-416.
3. Saerens, M., Fouss, F., Yen, L., & Dupont, P. (2004, September). The principal components analysis of a graph, and its relationships to spectral clustering. In ECML (Vol. 3201, pp. 371-383).
4. Sharma, A., Horaud, R. P., Knossow, D., & Von Lavante, E. (2009, November). Mesh Segmentation Using Laplacian Eigenvectors and Gaussian Mixtures. In AAAI Fall Symposium: Manifold Learning and Its Applications.