利用斷點迴歸設計設計估計需求曲線 – Uber 案例

一般而言，我們如果想要了解一項舉措 (treatment) 對使用者造成的影響，最佳的方法是「隨機控制實驗」(Randomized Control Experiment)。透過隨機控制實驗，我們能夠確保實驗組跟對照組除了該項舉措外沒有其他任何的差異，確保實驗組與對照組間的差異是因為該項舉措而產生。然而，並不是任何情況下都能夠透過隨機控制實驗來了解舉措對於使用者的影響，這件事情最常發生在「訂價」(pricing) 的問題上。想像你在搭 Uber 時，你跟你朋友間在同段時間與同段路程中被收取的費用不一樣時，你是不是會很生氣？為什麼他收到的比較便宜，我卻比較貴？

為了避免引發消費者的反感，我們要了解價格對消費者的影響時，時常會利用「自然實驗」 (Natural Experiment，又稱作擬實驗 Quasi-experiment) 的方法，在不做人為操作的情況下，製造近似隨機控制實驗的情況。今天我想跟大家介紹一個非常常見的自然實驗分析方法，叫做「斷點迴歸設計」(Regression Discontinuity Design，簡稱 RDD)。在這裡我使用了這篇論文作為案例：Using Big Data to Estimate Consumer Surplus:  The Case of Uber，是 Uber 分享他們怎麼透過 RDD 估計乘車市場的需求曲線，非常有趣喔！

Uber 的 Surge 訂價機制

Uber 在市場上很多人想搭車（需求），但司機（供給）不夠充足的情況下，會向消費者收取額外的費用。這個機制是，演算法會計算出一個 surge generator ，當消費者的 surge generator  是 1.5 x 時，車資就會變成原本的 1.5 倍。Uber 的 surge generator 其實會產生一個連續的數字，然後根據這個數字四捨五入，作為真正向使用者收取額外費用的 surge rate。比如說，當演算法產生的 surge rate 是 1.249 時，使用者當時的費率會變成原先的 1.2 倍；當產生的 surge generator  是 1.251 時， 使用者當時的費率會變成原先的 1.3 倍，出現了價格的跳躍。在此我們定義購買率為「搜尋路程」到「真正搭乘」的比率，則下列直方圖可以發現，在每一個 generator 會造成價格發生跳躍的時候，購買率都會呈現階梯狀的差異。

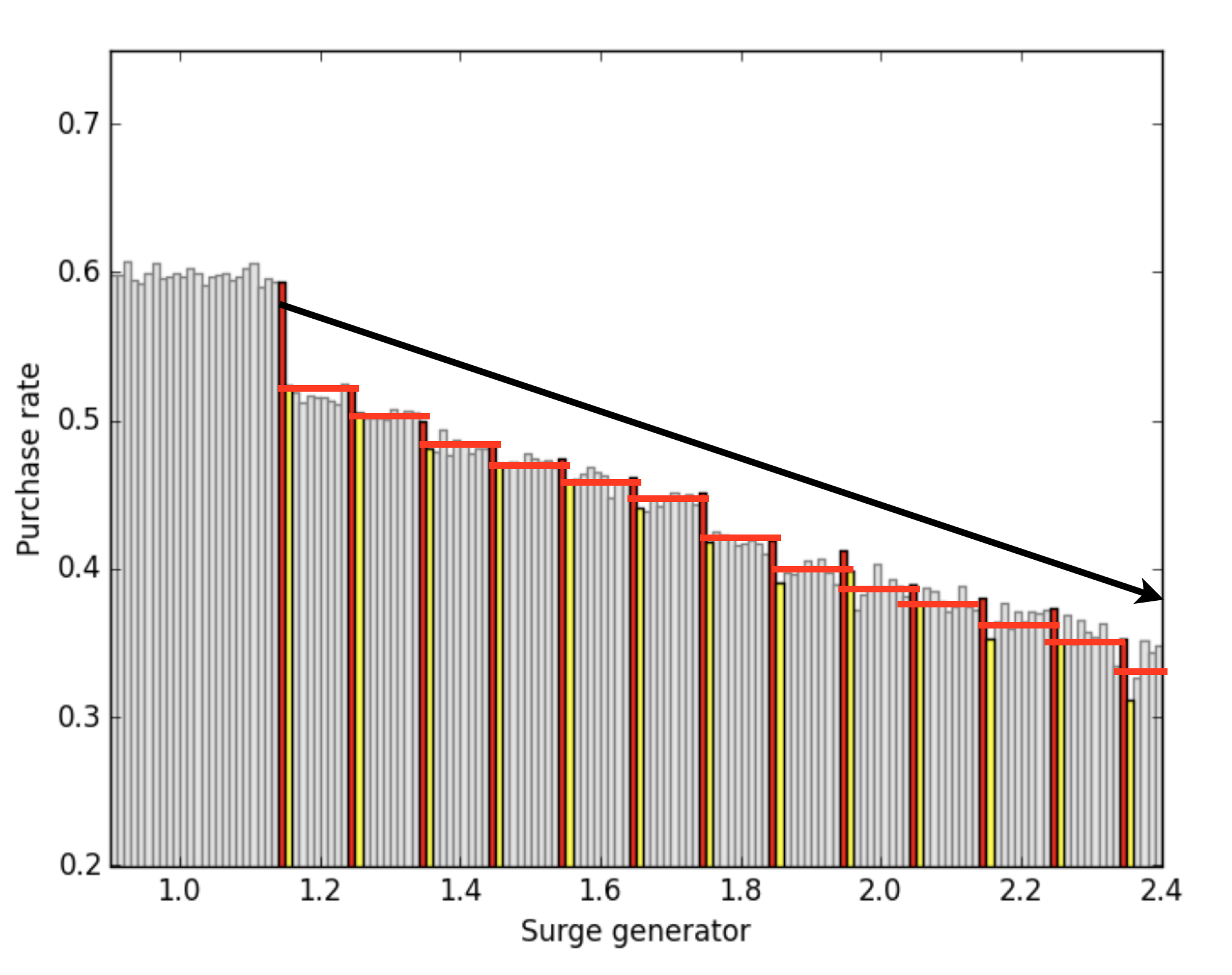
這樣造成了一個特殊的現象，當演算法產生 1.249 與 1.251 時，當時市場的供給需求環境可以說幾乎一樣，但卻有一部份的消費者是原先的 1.2 倍，另外一群則是 1.3 倍，產生了「近似於做了隨機控制實驗」的效果 – 一群使用者被分成高價位，另一群使用者則被分成低價位。這樣算起來，搭乘價格其實差了 10%，因此對於消費者的購買率造成了影響，該影響如下圖所表示。你可以發現，購買率與 surge generator 之間應該是連續的關係，卻在 surge generator = 1.25 x 時發生了不連續的跳躍，這就是我們為什麼我們稱這樣的概念為「斷點迴歸設計」- 本應為連續線性迴歸型態的資料，中途出現了不連續 (discontinuity) 的現象。

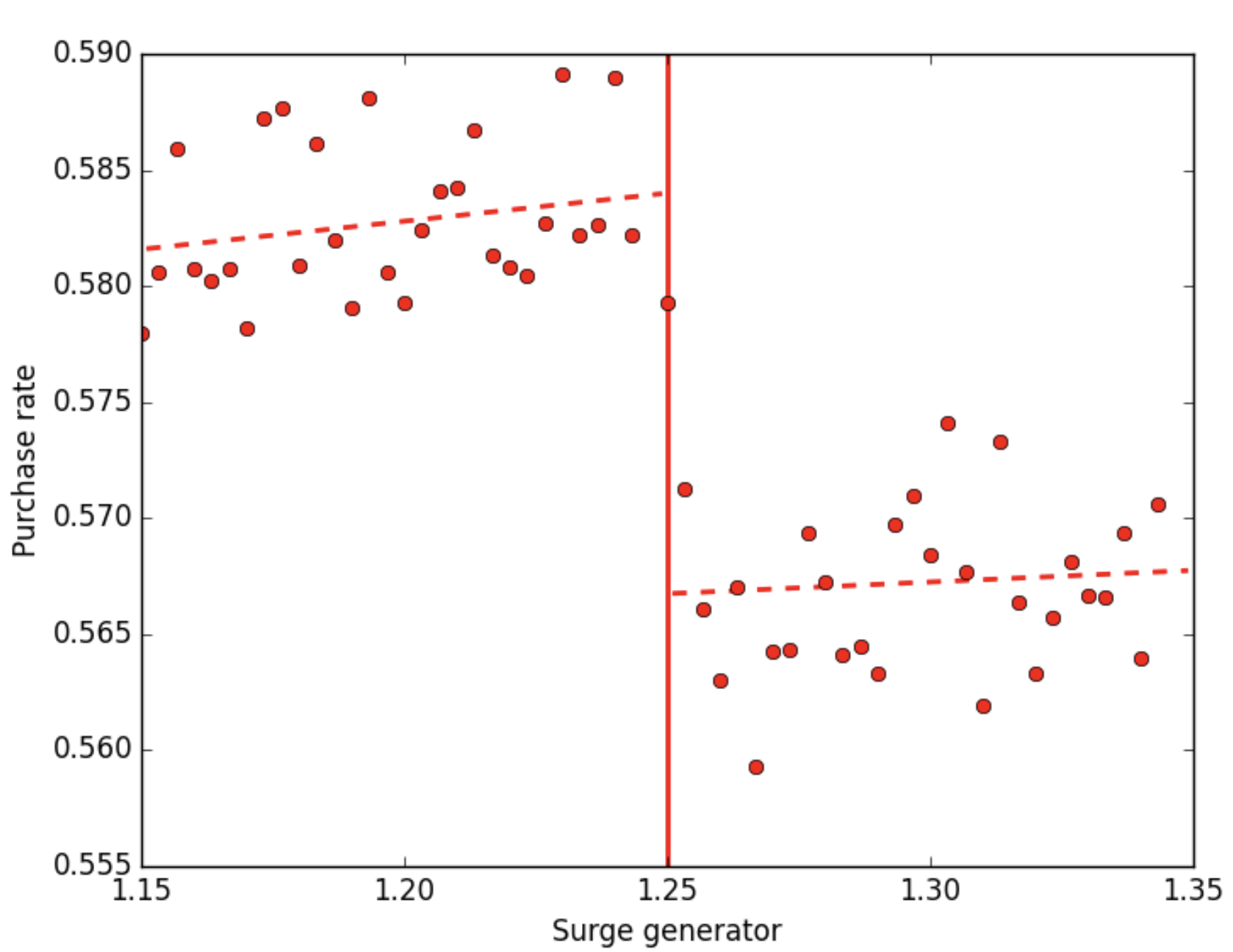
利用斷點迴歸設計估計價格彈性

當大家理解了斷點迴歸設計的概念後，我們接下來試著理解斷點迴歸設計的估計形式。定義  代表 surge generator 是否靠近不連續的地方（不夠靠近則不需要用來估計不連續處的影響）， 1 代表靠近 0 代表不靠近； 代表是否在不連續處 (如：surge generator 為 1.25) 右邊，其中 Post 代表 Post-discontinuity 的意思，1 代表在右側 (如：surge generator = 1.251 時 ) 0 代表在左側。 Uber 試圖建立以下迴歸模式：

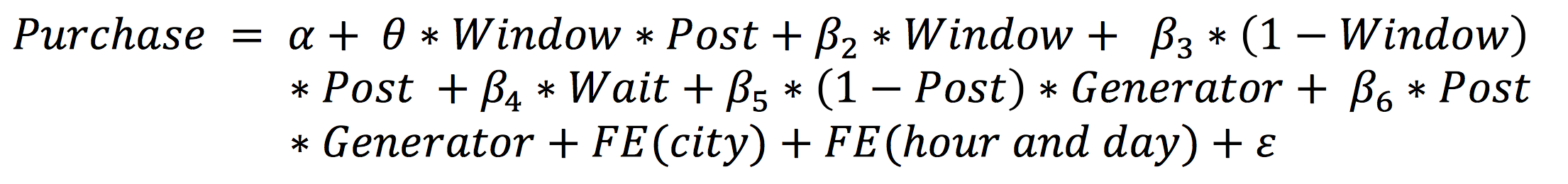
其中 代表預期等待時間， 代表的是 surge generator 的數值， 代表城市帶來的固定效果 (fixed effect)， 代表時段與日期等帶來的固定效果。

接下來，讓我們看看不連續處造成的自然實驗，會對  帶來什麼影響。假設等待等待時間、城市、時段與日期等都一樣，而且「是否在不連續處」並不會影響迴歸直線的截距 (也就是  )，那麼在不連續發生前後的迴歸直線斜率會如下所示。你可以發現，價格出現跳躍對於購買率造成的影響就是   。由此結果，我們可以推導出價格彈性(Price Elasticity, PE)： 。

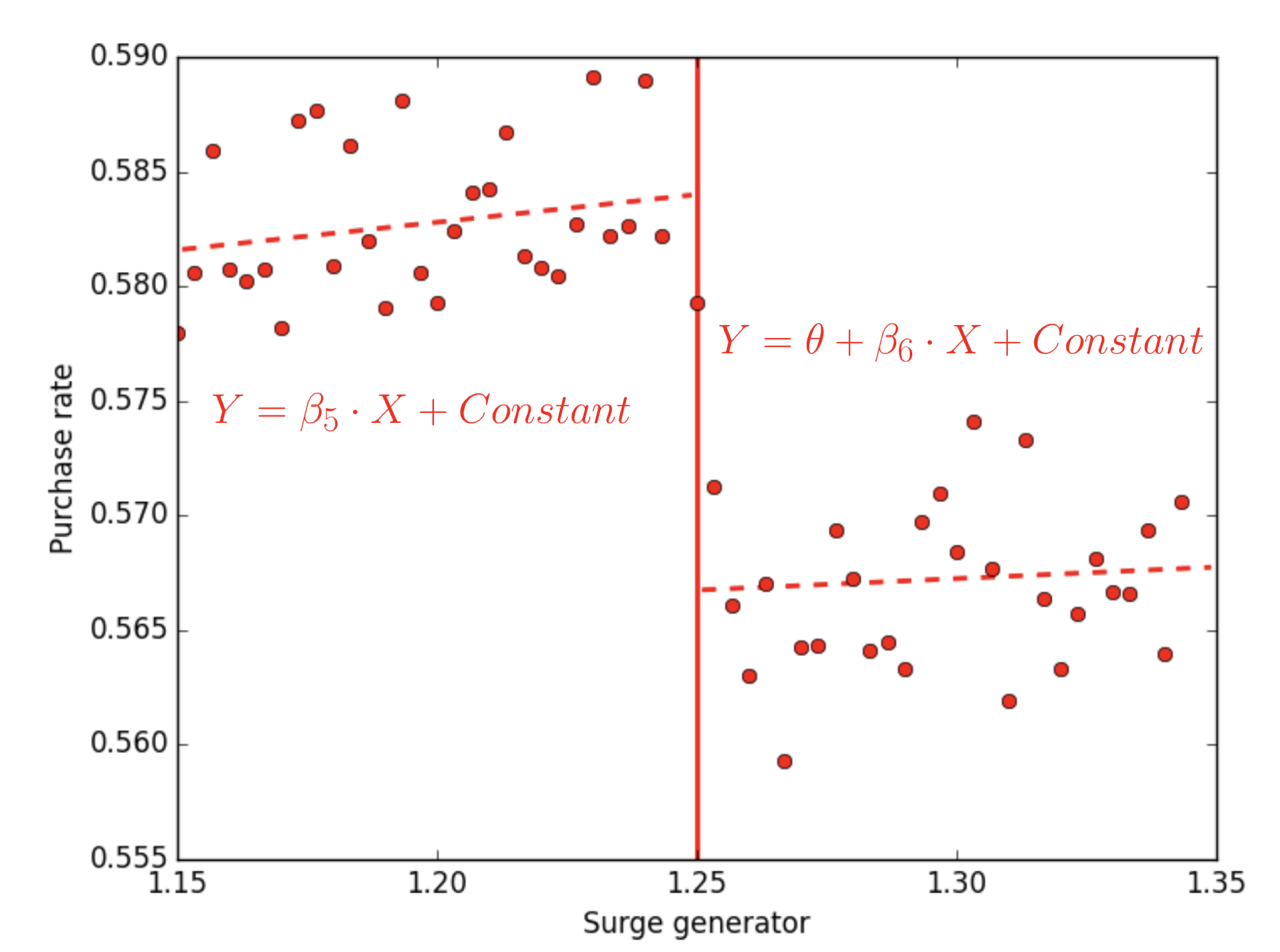
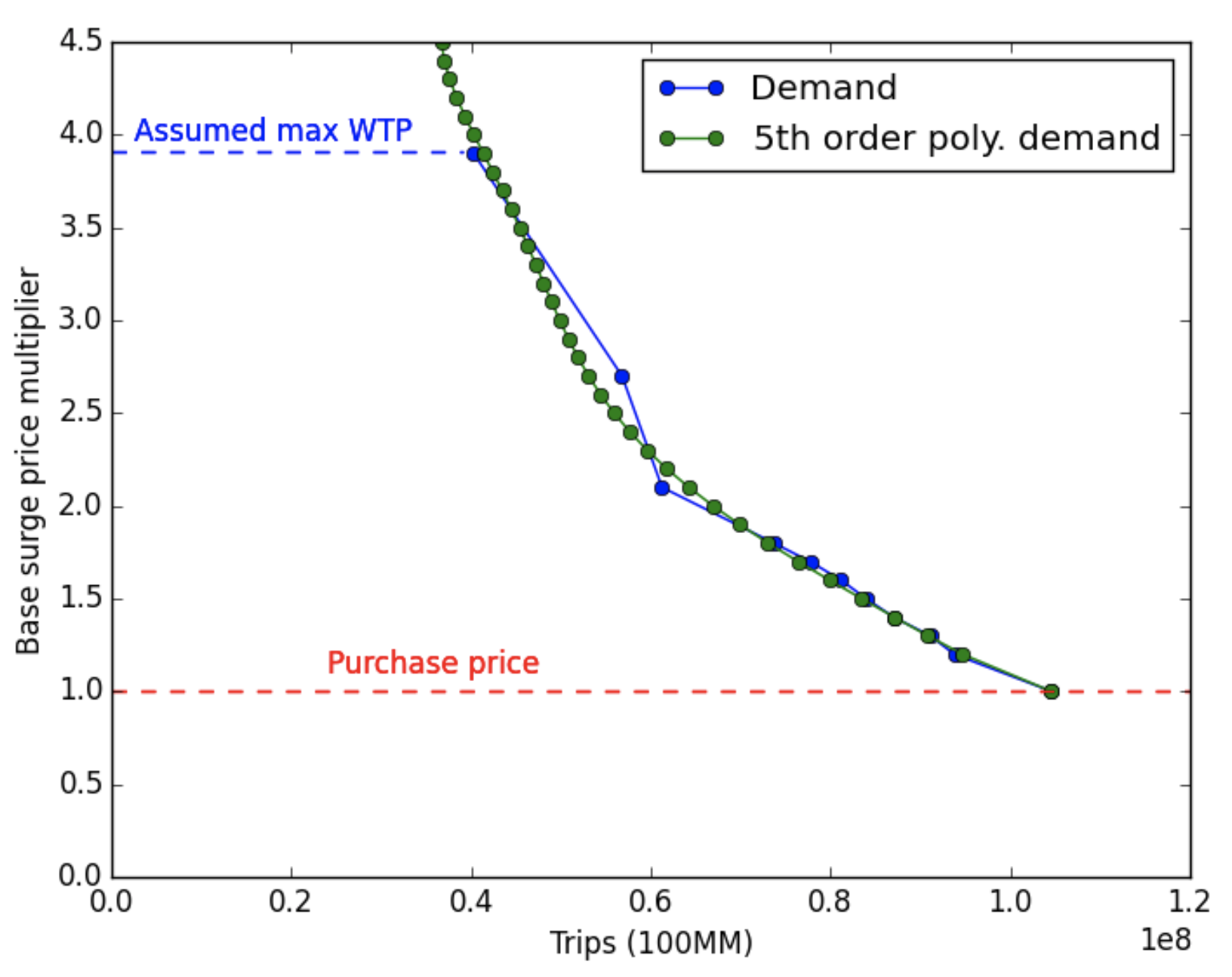
Uber 在每一個價格不連續 (e.g. 1.15, 1.25, 1.35, 1.45, …) 的附近，都做了一次上述的迴歸估計，如：1.1 – 1.2 估計一次，1.2 – 1.3 估計一次，計算出了不同的  值，以此推估價格彈性。接著透過價格彈性，可以估計出像是以下圖型的需求曲線 (Demand Curve)，反映價格 (Price) 跟總搭乘公里數 (Quantity) 間的關係。同時，也可以利用這條需求曲線，去計算不同類型的 surge generator 演算法，對於消費者剩餘造成的影響。

小結：規則常常就是一個自然實驗

其實斷點迴歸設計是一個在 1990 年代後就開始受到重視的計量經濟方法，尤其是政府政策，如：電價、稅率等，很難進行隨機控制實驗（找到兩組相似的個體給不同的價格）。然而，制定規則常常被用來使用的「門檻」，就是一個非常好的自然實驗。在斷點的左邊，是實驗的對照組 (control group)，在斷點的右邊則是實驗組 (treatment group)，這樣的自然實驗法，其實可以大量被運用在各種類型的問題，像是：會員忠誠度跟優惠折扣的關係等。斷點迴歸設計的模型辨別 (model identification) 跟估計方式也很有趣，希望之後有機會跟大家介紹。

有關 David’s Perspective 的最新文章，都會發布在大鼻的 Facebook 粉絲專頁，如果你喜歡大鼻的文章，還請您按讚或留言給我喔！

大鼻觀點：https://www.facebook.com/davidperspective/