完全了解 A/B 測試 ─ 只學初統也能做的資料分析 1

相信所有商學院的同學應該都修過一門既痛苦又不知道在幹嘛的課程─初等統計學，還記得我年少輕狂在修初等統計學時，因為是早上的課就時常睡過去 (汗)，考試前就把公式背一背就去考了…….當時很難意會到，其實初等統計學很多方法是很容易被應用在商業分析之中的，另外初等統計學中很多方法的重點不在公式或計算出答案，而是怎麼樣完成「設計實驗→蒐集資料→統計分析→得出觀點」的商業資料分析專案。因此，根據過去在專案中的經驗，我會挑選出幾個初等統計學常用的方法，並說說這些方法如何發揮在「使用者資料分析」與「行銷研究」之中。在第一篇的系列文中，我想聊聊「A/B 測試」，他在初等統計學中對應到的方法是「兩種樣本的假設檢定」 (two-sample hypothesis testing)，相信有學過初等統計學的人，可能…不一定有印象 😛

 A/B 測試 101 ─ 了解 A/B 測試的三個重點

為什麼 A/B 測試是重要的呢？根據 Google 內部的數據，被提出的改變只有 10% 能夠通過 A/B 測試，真正創造商業價值，而 Netflix 也提到依照直覺進行的決策有90%都是錯誤的。因此，這些大型網路公司通常會以數據為基礎，進行舊版本與新版本的測試，以確定新版本是真正能改善衡量指標，帶來商業價值。

在網路產業的大家，對於「A/B 測試」(A/B testing) 一定不陌生，但可能很少人知道 A/B 測試與統計學之間的關係。Conversion Lab 「AB測試第一次就上手～新手基礎篇」文章中對於 A/B 測試的定義是：

AB測試（A/B test）是許多網站、尤其是具備電子商務功能的網站拿來快速測試改版、微調效果並協助設計與商業決策的方法之一。簡單來說就是將欲測試的變因或假說分別做成A版與B版（甚至C、D等版），利用一些工具，將造訪網站的人流隨機均分至兩個版本，最後選擇目標達成表現較好的版本。

這個定義是正確的，但是一個簡化後的定義，為了以「統計」的角度來讓大家完全了解 A/B 讓我們再來看看維基百科上關於 A/B testing 的定義：

In marketing and business intelligence, A/B testing is a term for a randomized experiment with two variants, A and B, which are the control and variation in the controlled experiment. A/B testing is a form of statistical hypothesis testing with two variants leading to the technical term, two-sample hypothesis testing, used in the field of statistics.

從上面的定義，我們可以知道 A/B 測試其實包含了三個核心概念：「隨機化的實驗」、「一個變因，兩種選擇」、「兩種樣本的假設檢定」。以統計學中實驗設計的角度來看，進行A/B 測試實際上是在執行一個「隨機對照試驗」 (Randomized Controlled Trial，RCT)：在所有的使用者中隨機抽出兩組，一組投放 A 版本，另一組投放 B 版本，其中 A 版本與 B 版本只有一個地方不一樣，接著蒐集使用者的資料，並進行分析比較出哪一個版本較佳，這便是整個A/B 測試的過程。在進行 A/B 測試時的步驟如下：

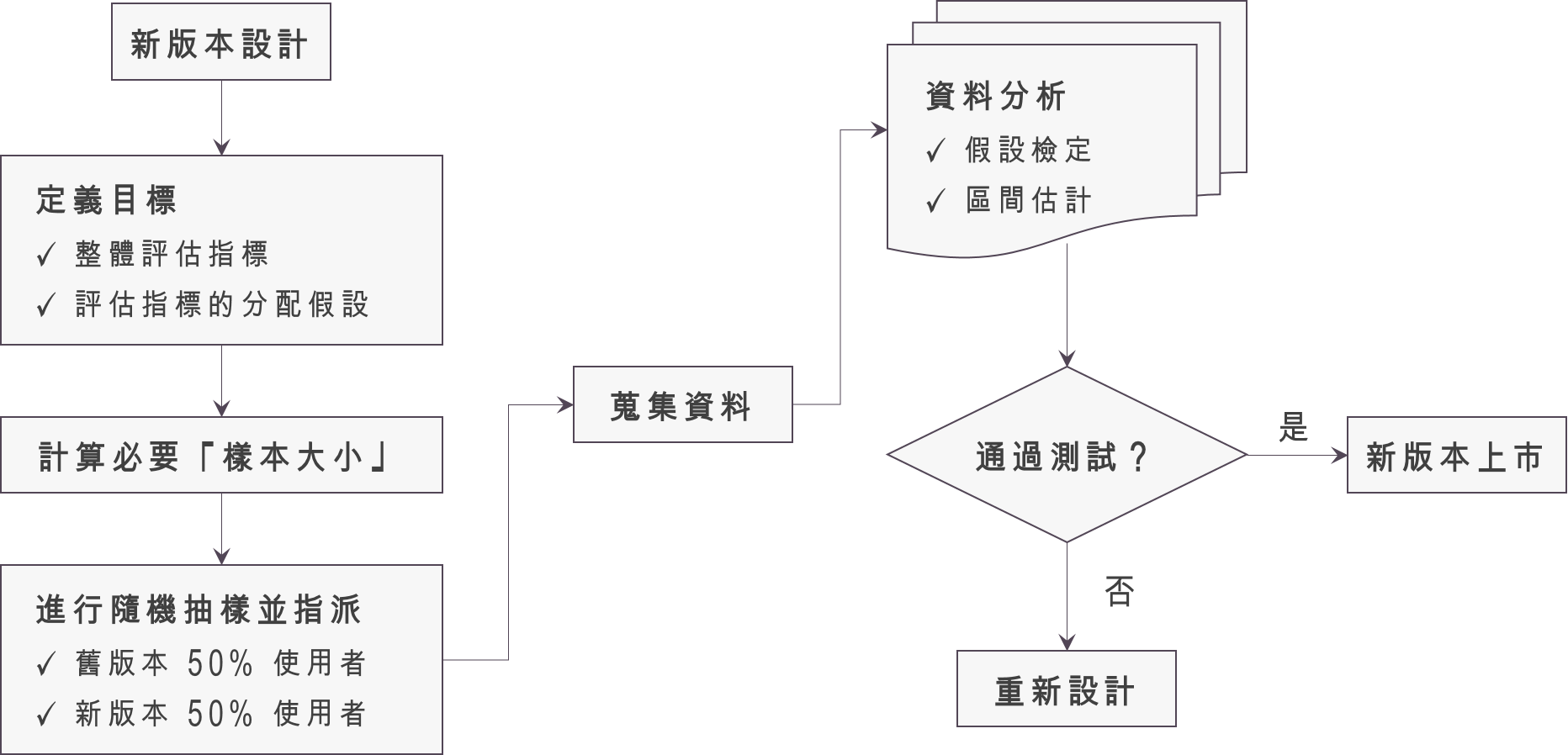
當產品設計出了新版本，想要比較新舊版本的差異時，應該要先定義「整體的評估標準」(overall evaluation criteria，OEC)，如：「付費使用者平均支付金額」、「付費使用者點擊率」、「付費使用者平均購買次數」等，在定義整體評估標準時，要注意該評估指標是否能真正衡量商業目標。在定義好整體評估標準時，我們需要對該 OEC 背後的分配假設，比如說：「付費使用者平均支付金額」我們會假設是常態分配(normal distribution)，「付費使用者點擊率」通常是運用白努力分配 (Bernoulli distribution)，「付費使用者平均購買次數」可能會假設是泊松分配 (Poison distibution)，假設分配有兩個目的，一是用於後面評估時的假設檢定與區間估計，二是計算「樣本數」的大小。不過，對於網路產業來說，樣本數的大小通常不是個大的問題，通常進行 A/B 測試只要 每個族群有 500 人時就可以了，比較需要進行樣本數計算的通常是醫學實驗。

隨機抽樣：來自「獨立」且「相同」的母體

接著就是要確認我們選取使用者時要選的足夠「隨機」，什麼樣叫做「隨機」呢？統計裡面對於「隨機樣本」的定義是：來自「相同」 (identical) 母體，且每次抽樣間互相「獨立」 (independent)。以「使用者點擊率」為例，我們蒐集到的資料會是舊版本第$latex j$個使用者的點擊與否 $latex X_{1j}$，以及新版本第$latex j$個使用者的點擊與否 $latex X_{2j}$，而這兩群我們都是選擇 $latex n$個使用者。在「隨機」的情況下，我們會假設 $latex (X_{11},\cdots,X_{1n}$ 為來自白努力分配的隨機樣本，其參數(點擊機率) 為 $latex p_{old}$， $latex (X_{21},\cdots,X_{2n}$ 為來自白努力分配的隨機樣本，其參數(點擊機率) 為 $latex p_{new}$，而 A/B 測試便想確認 $latex p_{new}$ 是否顯著大於 $latex p_{old}$。

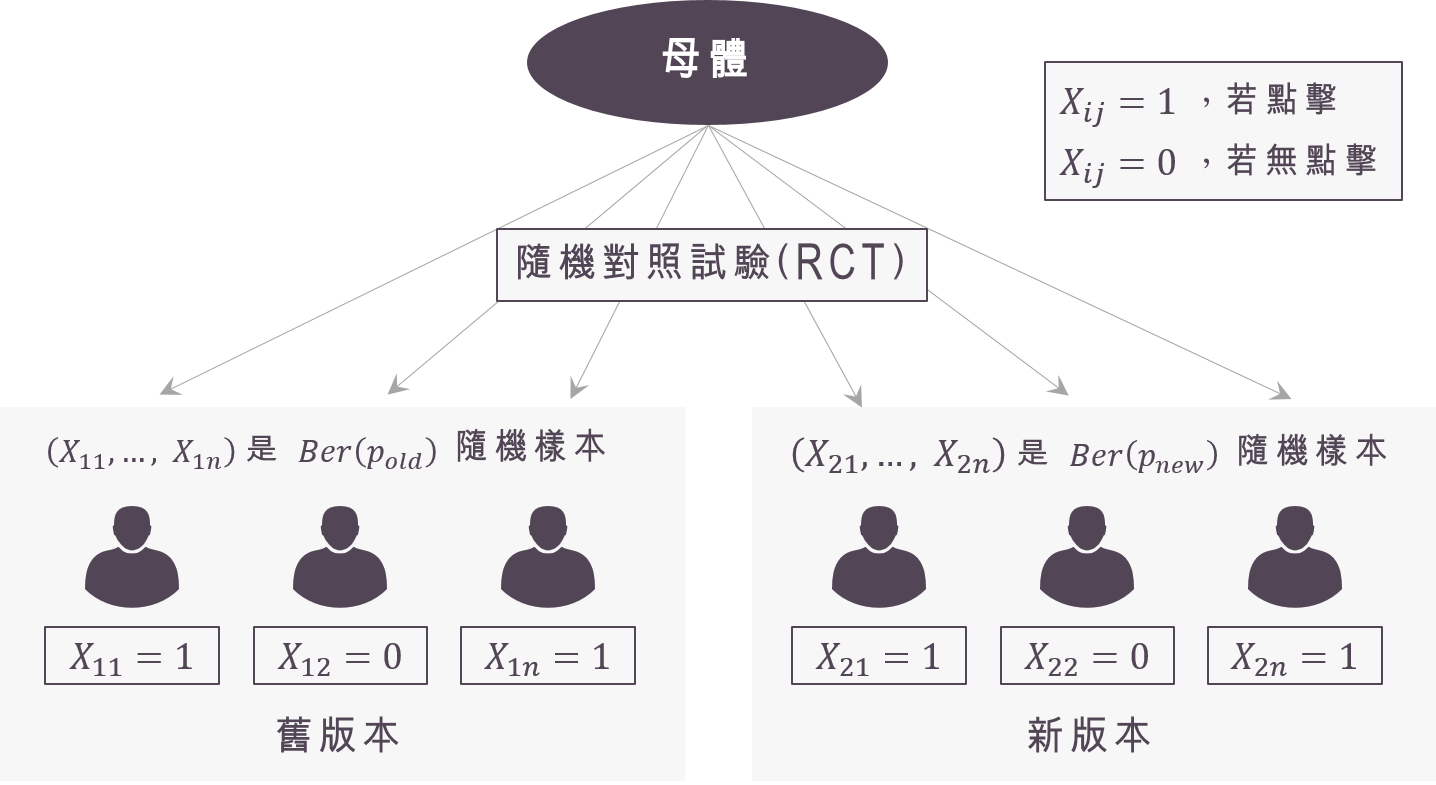
「隨機」的好處在於：如果樣本數夠大且足夠隨機，照理來說我們每個類型的使用者都會抽到，因此就算每個個體都會有差異，隨機抽樣將會幫我們把個體的差異抵銷掉，因而能夠看出新舊版本間的平均差異。當然，這樣的概念還是會有風險，因此我們會接著進行下一步的統計檢定與區間估計。

統計分析：辨認「實際差異」與「隨機誤差」

前面提到，「隨機抽樣」雖然能夠抵銷潛在因素造成的影響，但我們並不能確認觀察到的新舊版本差異 $latex p_{new}-p_{old}$ 是「實際差異」，還是因為隨機抽樣或是誤點造成的「隨機誤差」 (random error)，因此我們會透過統計中的「假設檢定」或「信賴區間」，辨別觀察到的差異究竟是「實際差異」還是「隨機誤差」。以 $latex p_{new}-p_{old}$ 的例子來說，會進行「兩樣本比例」的比較分析，如果有興趣的朋友可以去閱讀 Comparing Two Proportions 一文。

在初等統計學中教過很多假設檢定的方法，其實都可以應用在此處。「付費使用者平均支付金額」可以進行「獨立樣本 t 檢定」(independent sample t test)，「付費使用者點擊率」可以進行「兩樣本比例 Z 檢定」(two-sample proportional Z test)，若不想進行分配假設，也可以使用無母數的Mann–Whitney U test，如果想要進行多個版本的測試，也可以使用「卡方檢定」(Chi-squared test)。這些檢定其實可以運用 EXCEL 的「分析工具箱」進行分析，可以見「台大統計教學中心初等統計學教材」。

注意：每次測試只能測試「一個因子」？

在結束這篇文章之前，特別要談到的是，在進行 A/B 測試時應當要盡量只測試一個因子，比如說：如果想要測試按鈕的顏色，就不要改變頁面文字，才不會無法分辨顏色變化或頁面文字變化的效果。但是，如果是希望測試「按鈕的顏色」與「性別」間的交互關係，我們仍然可以設計統計方法進行分析，比如說：初等統計學中的雙因子變異數分析(two-way ANOVA)。

希望看完這篇文章的朋友，能夠體會到初等統計學所教授的內容是可以實際應用到商業問題的。做資料分析並不一定要很難的數學模型，或寫很大架構的程式，只要你了解並用對統計方法，就能有效地進行資料分析。在學習初等統計學時，重點其實要放在統計方法背後的「分析架構」，而不是著重在公式或計算，這樣才能夠將學到的統計方法應用在實務中。

有關 David’s Perspective 的最新文章，都會發布在大鼻的 Facebook 粉絲專頁，如果你喜歡大鼻的文章，還請您不吝嗇地按讚或留言給我喔！

大鼻觀點：https://www.facebook.com/davidperspective/