利用 RBP / RBA 設計衡量定位策略 (Targeting Policy) 的成效

「精準行銷」(Precision Marketing) 是這十年來行銷領域相當熱門的話題，比如說：當用戶決定終止目前的電信合約轉換到另一家廠商時，可否依照使用者族群設計專屬的續約優惠；或者是外送平台可能會「依據你過去的使用情況進行分群」，針對不同族群提供不同類型的當月優惠活動；又或者是 Netflix 在進行個人化推薦時，應該要以「與用戶來自相同國家的使用者」作為模型訓練依據，或是要以「平台上所有用戶」作為訓練資料呢？對於行銷人員來說，如何有效衡量不同的策略，進而節約行銷預算做到真正有效的精準行銷，一直都是很大的問題。因此，今天想跟大家分享一篇最近刊登在 Management Science 上的論文—— Efficiently Evaluating Targeting Policies: Improving Upon Champion vs. Challenger Experiments。

定位策略 (Targeting Policy) 與表現衡量

上面這些例子都可以看到，在做精準行銷時會有「指派」的動作：依據不同的定位策略 (targeting policy，比如說：不同的行銷活動規則、不同的預測模型等)，讓使用者收到對應的行動 (action，比如說：9 折優惠 vs. 7 折優惠、先顯示國家 top 10 觀看電影 vs. 個人化的推薦名單等)。由量化模型的角度出發，假設這次實驗的客戶樣本 $latex h = 1,\cdots, H$ 來自用戶母體 $latex \mathcal{H}$，每個用戶的特徵計為 $latex \mathbf{x}_h$，所有可能的行銷行動所形成的集合為 $latex \mathcal{A}$，則定位策略 (targeting policy) $latex \mathcal{P}: \mathcal{H} \rightarrow \mathcal{A}$ 是一個將客戶指派給某個行銷活動的函數。

在衡量一個特定的定位策略成效時，常常會以該定位策略帶來的平均每位客戶收益為衡量指標，以數學式表達為：

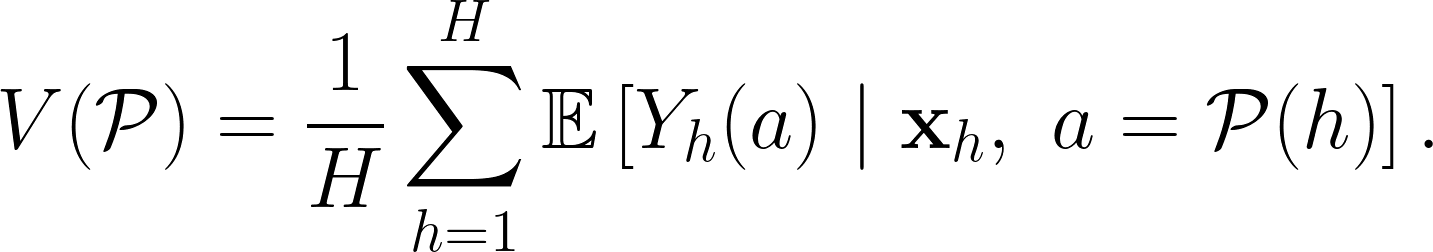
在論文中考慮的是最簡單的 $latex Y_h(a)$ 形式——實際表現由三個因素所決定，一是行銷行動的平均表現，二是用戶個別的表現，三是隨機誤差，因此我們可以建立線性迴歸模型：

RBP 設計與 RBA 設計

為了衡量不同定位策略的表現，有些公司會透過隨機控制實驗 (randomized controlled experiment) 來衡量定位策略與行銷行動的成效。其中  RBP 設計 (Randomized by Policy) 的處置是「定位策略」，也就是每一個客戶會收到一個定位策略，該策略會決定該客戶收到什麼樣的行銷行動。另一種類型的衡量方法是 RBA 設計 (randomized by action) ：將客戶隨機分組後，每一組用戶直接隨機指派一個行動。

因此，公司針對這 $latex H$ 個樣本進行隨機實驗時，其實是在進行「指派」(assignment)——不論是指派一個定位策略 (下面提到的 RBP 設計) 或是一個行動 (下面提到的 RBA 設計)。令客戶 $latex h$ 收到的指派為 $latex W_h$，由於是隨機實驗，所以 $latex W_h$ 應該與 $latex \mathbf{x}_h$ 互相獨立。進行實驗後，不論是 RBP 或是 RBA，客戶都會收到一個行銷行動 $latex a$，因此客戶 $latex h$ 的表現 $latex Y_h (a)$ 是一個行銷活動 $latex a$ 的函數。

在 RBP 設計下，客戶 $latex h$ 收到的指派是某個策略 $latex \mathcal{P}_W$，也就是 $latex W_h = \mathcal{P}_W$，而指派的策略 $latex \mathcal{P}_W$ 會選擇一個行銷行動給客戶 $latex h$，因此實際上觀察到的客戶表現 $latex Y^{obs}_h$ 其實是隨機變數 $latex Y_h (a),~a = \mathcal{P}_W(h)$ 產生的結果。而 RBA 設計下，客戶 $latex h$ 收到的指派是某個行動 $latex a_W$，也就是 $latex W_h = a_W$，而 $latex Y^{obs}_h$ 則是隨機變數 $latex Y_h (a_W)$ 產生的結果。由上述可以知道，RBP 設計的指派數為待衡量策略的數量，計為 $latex T$，而 RBA 設計可能的指派數量則為可能的行銷行動數 $latex |\mathcal{A}|$。

衡量時先考量單一策略 $latex \mathcal{P}$ 的評估方式。實際上觀察到的樣本為 $latex (Y^{obs}_h, W_h)$，因此不論當初是以RBP 設計與 RBA 設計指派行動，我們都能夠建立 $latex \mathcal{P}$ 的衡量樣本。如果當初是 RBP 設計，則 $latex \mathcal{P}$ 的衡量樣本為 $latex D^{RBP}_{\mathcal{P}}=\{h: W_h = \mathcal{P} \}$，也就是實驗指派為 $latex \mathcal{P}$ 的樣本；而 RBA 設計的樣本則為 $latex D^{RBA}_{\mathcal{P}}=\{h: \mathcal{P}(h) = W_h \}$，也就是實驗指派行動跟 $latex \mathcal{P}$ 建議行動一致的樣本，衡量該政策表現的公式為 $latex V(\mathcal{P}) =\frac{1}{D^{\cdot}_{\mathcal{P}}} ~\sum_{h\in D^{\cdot}_{\mathcal{P}}} Y^{obs}_h$。

在比較不同策略時，如果是依照「各個策略的使用者加總計算成效」，可能會有些問題。首先，因為每個行動 (action) 本身的平均效益不同，而且不同策略可能會有較高的機率指派某一個特定的行動，因而產生辛普森悖論 (Simpson’s Paradox)——不確定是某個策略表現好是因為策略奏效，還是是因為該策略容易指派到表現較佳的行動 (e.g. 一直指派七折優惠券而非九折優惠券)。此外，在計算差異時是使用所有客戶進行評估，此時可能會遇到不同策略推薦相同行動的情況，即使該用戶側

不同策略的樣本建立與成效評估

假設現在我們想要衡量兩個不同的策略  $latex \mathcal{P}_1$ 與  $latex \mathcal{P}_2$，傳統的衡量方式是直接計算 $latex V(\mathcal{P}_1) – V(\mathcal{P}_2)$，但在這樣的估計模式中，但由於很可能同兩個策略可能都會對同一個用戶推薦同樣的行動，因此這篇文章建議只衡量「 $latex \mathcal{P}_1$ 與  $latex \mathcal{P}_2$ 推薦不同策略時」的差異，也就是：

在估計差異時，考慮以最簡單的線性模型 $latex Y_h = \alpha + \gamma \cdot \mathbf{1}_{\mathcal{P}_1}+ \boldsymbol\beta \cdot \mathbf{x}_h +\varepsilon_h$ ，其中 $latex \mathbf{1}_{\mathcal{P}_1} = 1$ 代表客戶 $latex h$ 收到的行動與 $latex \mathcal{P}_1$ 的推薦一致， $latex \mathbf{1}_{\mathcal{P}_1}=0$ 則代表客戶 $latex h$ 收到的行動與  $latex \mathcal{P}_1$ 的推薦不同。

為了有效評估兩組策略的不同，我們可以將測試客戶分為「收到相同推薦的族群」與「收到不同推薦的族群」。在 RBP 設計下，「收到相同推薦的族群」為 $latex \{h:~W_h \in \{\mathcal{P}_1, \mathcal{P}_2\},~\mathcal{P}_1 (h) = \mathcal{P}_2 (h)\}$，而「收到不同推薦的族群」為 $latex \{h:~W_h \in \{\mathcal{P}_1, \mathcal{P}_2\},~\mathcal{P}_1 (h) \neq \mathcal{P}_2 (h)\}$。同理，在 RBA 設計情況下我們一樣可以區分「收到相同推薦的族群」$latex \{h:~W_h = \mathcal{P}_1 (h) = \mathcal{P}_2 (h)\}$ 與「收到不同推薦的族群」 $latex \{h:~W_h =\mathcal{P}_1 (h) \neq \mathcal{P}_2 (h)\} \bigcup  \{h:~W_h =\mathcal{P}_1 (h) \neq \mathcal{P}_1 (h)\}$（也就是「指派行動和策略 1 推薦一致，和策略 2 推薦不一致」與「指派行動和策略 2 推薦一致，和策略 1 推薦不一致」的客戶）。

上述的樣本建構中，「收到相同推薦的族群」不會貢獻任何資訊給「兩組策略的成效差異」，因此我們只需要使用「收到不同推薦的族群」的客戶資料進行建模即可。而上述線性模型中的 $latex \gamma$ 就代表「$latex \mathcal{P}_1$ 比  $latex \mathcal{P}_2$ 多 (或少) 帶來的好處」。因此可以得到兩者成效差異 (也就是 average treatment effect) 的估計式與標準誤 (standard error)：

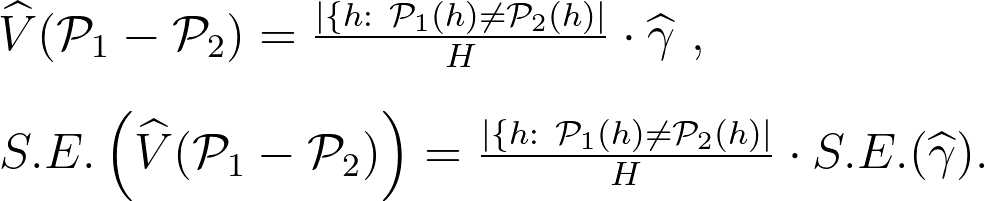
除了用上述的估計方法外，我們也可以用 $latex V(\mathcal{P}_1-\mathcal{P}_2) = \frac{1}{H}\sum_{h:~ \mathcal{P}_1 (h) \neq \mathcal{P}_2 (h)} \mathbb{E}[Y_h~|~\mathbf{x}_h, \mathcal{P}_1(h)] –  \mathbb{E}[Y_h~|~\mathbf{x}_h, \mathcal{P}_2(h)]$ 的估計式得到 average treatment effect，可以見論文的 Appendix （概念上很簡單）。

小結：衡量定位策略 (Targeting Policy) 的成效

個人讀完這篇論文的感想是：雖然論文本身概念上挺簡單的，而且沒有什麼方式去證明這些方法的收斂性與好壞，但這的確是一篇可以開啟很多研究主題的論文，尤其是跟 Reinforcement Learning 各種類型的 policy evaluation ，從理論研究到實務應用都是非常有啟發性的論文！

有關 David’s Perspective 的最新文章，都會發布在大鼻的 Facebook 粉絲專頁，如果你喜歡大鼻的文章，還請您按讚或留言給我喔！

大鼻觀點：https://www.facebook.com/davidperspective/