人工智慧與增強學習 1：什麼是增強學習？

「大鼻觀點」粉絲團：https://www.facebook.com/davidperspective/

暑假在優拓資訊實習時，我第一次接觸了「增強學習」 (reinforcement learning) ，當時雖然只花了一個禮拜研究，但在這之後我覺得相當有趣，因此想花點時間來研究這個主題。碎碎念一下，我覺得這個領域讓我覺得有興趣的原因有兩個，一是我非常喜歡「決策」類的議題，像是財務裡面被廣為應用的「平賭過程」 (martingale)，就會有研究最佳停止時間 (optimal stopping time) 的議題；二是我自己著墨比較深的領域是時間序列分析 (time series analysis)，我覺得隨機過程、時間序列跟增強學習的建模概念非常非常像，都是屬於「序列決策模型」 (sequential decision model)。為了逼自己研究，決定把它寫成文章，將我的學習成果分享給大家。因為這是大鼻第一次接觸這個領域，如果有錯誤的地方還請大家多多指教，謝謝！

「增強學習」：讓機器學習「進行決策」的方法

增強學習是機器學習領域非常特別的問題，是「人工智慧」 (artificial neural network) 領域中相當重要的議題，他的概念是這樣的：人類在進行決策時，常常會根據目前「環境」(environment) 的「狀態」 (state)   執行「動作」 (action)，執行動作會造成兩個結果：一是人們會得到「環境」給我們的回饋，也就是人類會得到「報酬」 (reward) ，接著我們所執行的動作也會去改變「環境」，使得「環境」進入到一個新的「狀態」。一般人會根據「環境」給予的「報酬」，修正自己執行的「策略」，試圖極大化自己的「長期報酬」。增強學習希望讓機器，或者稱為「代理人」 (agent)  ，模仿人類的這一系列行為。說到這裡頭有點暈，因此我們可以用以下這張圖來說明剛剛講的過程：

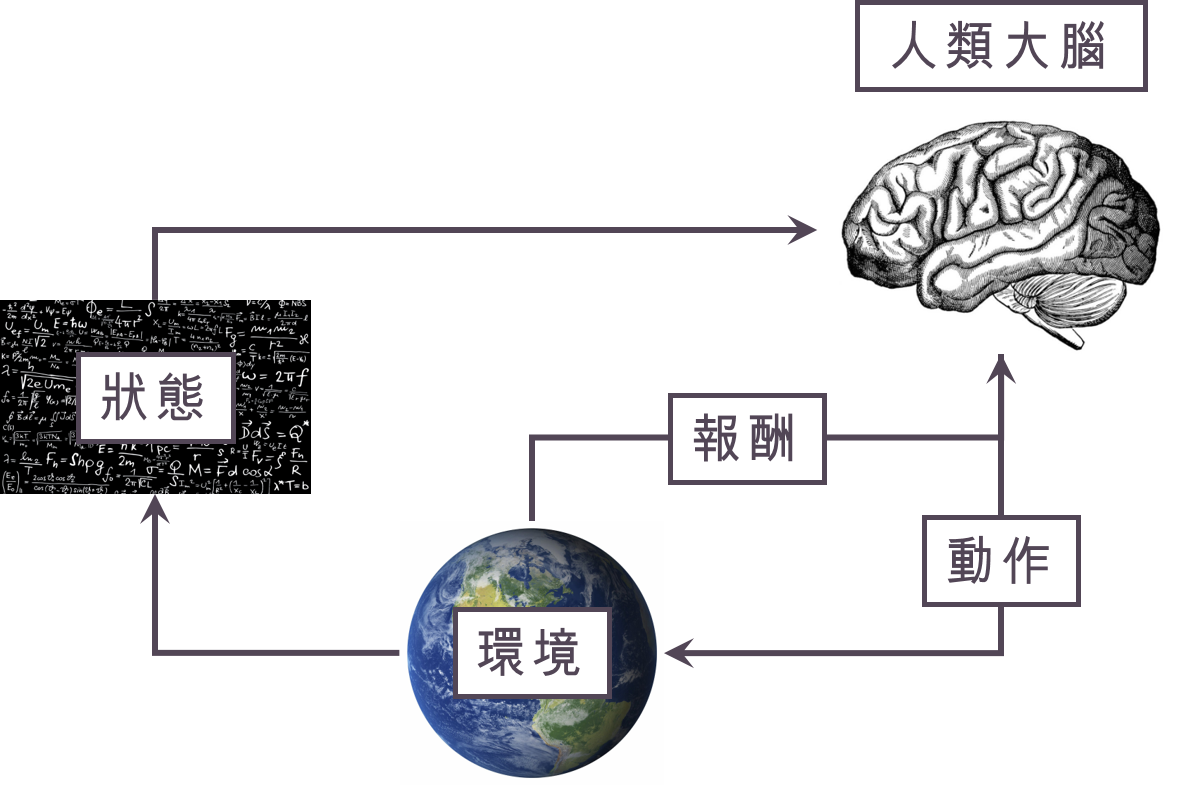
「觀察到目前的狀態→執行動作→收到報酬與觀察到新的狀態」這樣的步驟可能會重複非常非常多次，直到某個終止時間 (stopping time)，接著我們用更正式的數學語言來表達以上的情境。假設在時間點 $latex t = 0, 1, 2, 3, \cdots$ (離散時間) 代理人將需要執行動作，在 $latex t$ 時間點觀察到目前「狀態」的表達式 (representation)  $latex \mathbf{S}_t \in \mathcal{S}$，其中  $latex \mathcal{S} $代表所有可能的「狀態」表達式所構成的集合。根據目前收到的狀態 $latex \mathbf{S}_t$，代理人將會執行「動作」  $latex   A_t  \in \mathcal{A}\left(\mathbf{S}_t\right)$ ，其中  $latex \mathcal{A}\left(\mathbf{S}_t\right) $  代表的是在目前狀態為  $latex \mathbf{S}_t$  下，代理人可以執行的所有動作所構成的集合。在執行動作後，代理人會知道「環境」所給予的「報酬」  $latex R_{t+1}$  以及新的狀態  $latex \mathbf{S}_{t+1}$，值得注意的是，   $latex (\mathbf{R}_{t+1}, \mathbf{S}_{t+1}) $是被同時決定的，也就是說   $latex (\mathbf{R}_{t+1}, \mathbf{S}_{t+1}) $  有聯合分配 (joint distribution)。

「代理人」的組成：政策、價值函數、模型

在增強學習的序列決策過程中，一個好的「代理人」將要具備三項元素：政策 (policy) 、 價值函數 (value function)、以及模型 (model)。「政策」，通常記為 $latex \pi$，指的是代理人執行「動作」的根據，比如說：「執行能夠使價值函數極大化的動作」是一種常見的「政策」，另一種常見「政策」叫做 $latex \epsilon$-greedy 演算法，先給定一個在  $latex (0,1)$  區間內的數  $latex \epsilon$ ，有  $latex \epsilon$ 的機率「代理人」會隨機執行一個「動作」，有  $latex 1-\epsilon$  的機率「代理人」會執行能夠使價值函數極大化的「動作」。

接著，我們要討論什麼叫做「價值函數」。假設現在處在時間點  $latex t$，我們有「狀態表達式」   $latex \mathbf{S}_t$，「代理人」有一個給定「折現因子」 $latex \gamma$，目前使用的「政策」是 $latex \pi$，則「價值函數」是給定  $latex \mathbf{S}_t$ 未來所有的「條件期望報酬」折現至現在的總和，也就是財務領域中的「淨現值」(net present value)，其數學表達式如下：

$latex v_{\pi}( \mathbf{S}_t) = \mathbb{E}_{\pi}(R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots |  \mathbf{S}_t)$。

實際上，「價值函數」是未知的，因此我們需要透過不斷「執行動作並收到報酬」蒐集資料，並用蒐集到的資料來估計「價值函數」。「價值函數」的估計方法有很多，比如說：動態規劃 (dynamic programming) 、 蒙地卡羅法 (Monte Carlo method)、或是當時差分法 (temporal difference method)，這些方法在日後會逐一介紹。

最後，要跟大家聊聊什麼是「模型」。「模型」是預測「環境」走勢的方法，在增強學習的設定中，「環境」在「代理人」執行「動作」後有兩種行為，一種是「狀態」的變化，一種是「報酬」的給予，因此「模型」想要試著刻劃：

1. 給定時間點 $latex t$ 的「狀態」表達式 $latex  ~\mathbf{S}_{t}=\mathcal{S}~$，「代理人」執行的「動作」 $latex  A_t=a$，下一個時點「環境」所處在的「狀態」表達式是$latex ~ \mathbf{S}_{t+1}=\mathcal{S}’~$的條件機率，數學表達式為：$latex \mathcal{P} _{\mathcal{S},\mathcal{S}’}^{a} =\mathbb{P}(\mathbf{S}_{t+1}=\mathcal{S}’|\mathbf{S}_{t}=\mathcal{S},A_t=a)$。
   $latex ~~$
2. 給定時間點 $latex t$ 的「狀態」表達式 $latex  ~\mathbf{S}_{t}=\mathcal{S}~$，「代理人」執行的「動作」 $latex  A_t=a$，所收到的期望報酬，數學表達式為：$latex \mathcal{R}_{\mathcal{S}}^a = \mathbb{E}(R_{t+1}| \mathbf{S}_{t}=\mathcal{S},A_t=a)$。

小結：邊走邊學的增強學習

所有的增強學習演算法都有一個共同的特色，就是「邊走邊學」，增強學習演算法可能要讓「代理人」去學「政策」、「價值函數」、「模型」，可能只學一種，也可能都學。因此我們會讓「代理人」不斷的去執行動作，累積經驗，所以我認為增強學習其實就是邊走邊學。

小朋友在學走路的時候會怎麼學呢？他可能會有非常多不同的走法，小步走、顛起腳尖走、往後倒退、往左走、往右走、大步走等各種不同的「動作」，當「環境」處在平坦、樓梯、有障礙等不同的「狀態」時，小朋友會需要「探索」(explore) 不同的「動作」，但同時又不能跌倒太多次，希望他走得很順利，也就是要「發揮」(exploit)。一個好的增強學習演算法，要能夠使小朋友，也就是「代理人」學得好，應當要能夠適當的平衡「探索」的成本與「發揮」得到的報酬。

在下一篇文章中，我會分享一個比較簡化的「增強學習」問題，叫做「吃角子老虎機」 (bandit) ，並簡單介紹一個很常被使用的演算法─信賴上界法 (upper confidence bound， UCB)，更深入討論探索 (exploration)與發揮(exploitation)。有關 David’s Perspective 的最新文章，都會發布在大鼻的 Facebook 粉絲專頁，如果你喜歡大鼻的文章，還請您不吝嗇地按讚或留言給我喔！