讀者提問：什麼是支持向量機 (SVM)

幾乎所有的機器學習課程，都會談到一個很經典的演算法，叫做支持向量機 (support vector machine) 。要應用支持向量機在實際問題上非常容易，台大資工系林智仁老師實驗室開發的「LIBSVM」有非常多不同語言的接口，如：R語言的範例，但背後的數學及最佳化理論倒是滿複雜的，剛好最近有個朋友在粉絲專頁上問到，「支持向量機到底是什麼？」所以我想要(嘗試) 用比較好理解的方法簡單介紹什麼是 SVM。

在開始正式談 SVM 之前，想先定義一下在這篇文章中的範例，假設今天的目的是研究信用卡的違約情況，我們定義 $latex ~Y~$ 代表是否違約，$latex ~Y=1~$代表該客戶違約，$latex ~Y=-1~$代表客戶沒有違約。銀行蒐集了每一個客戶的兩個變數，$latex ~X_1~$記錄著客戶的年收入，$latex ~X_2~$記錄著客戶的淨資產價值。銀行想透過 $latex ~\mathbf{X} = (X_1,X_2)~$ 這兩個變數來預測$latex ~Y~$，是一個非常典型的「分類」 (classification) 問題。假設銀行現在有 $latex ~N~$ 個客戶的資料 $latex (\mathbf{X}_i,Y_i),$ $latex i = 1, \cdots, N$ 作為機器的訓練集合 (training set)。

「線性可分集合」(Linearly Separable Set)

在開始談 SVM 之前，我們先來談談最簡單的情形，也就是我們的訓練集合是「線性可分集合」(linearly separable set)，聽起來好像很可怕，我們可以用下圖來解釋：圖中橫軸代表 $latex ~X_1~$，縱軸代表 $latex ~X_2~$，而藍色的點代表沒有違約的客戶，也就是 $latex ~Y=-1~$ 的樣本點，紅色的點則代表違約的客戶，也就是 $latex ~Y=1~$ 的樣本點。簡單來說，如果能夠用一條直線就把紅色與藍色的點分開，則代表我們蒐集的訓練集合是線性可分的，若沒辦法只用一條直線就把紅色與藍色的點分開，則代表我們蒐集的訓練集合是線性不可分的。

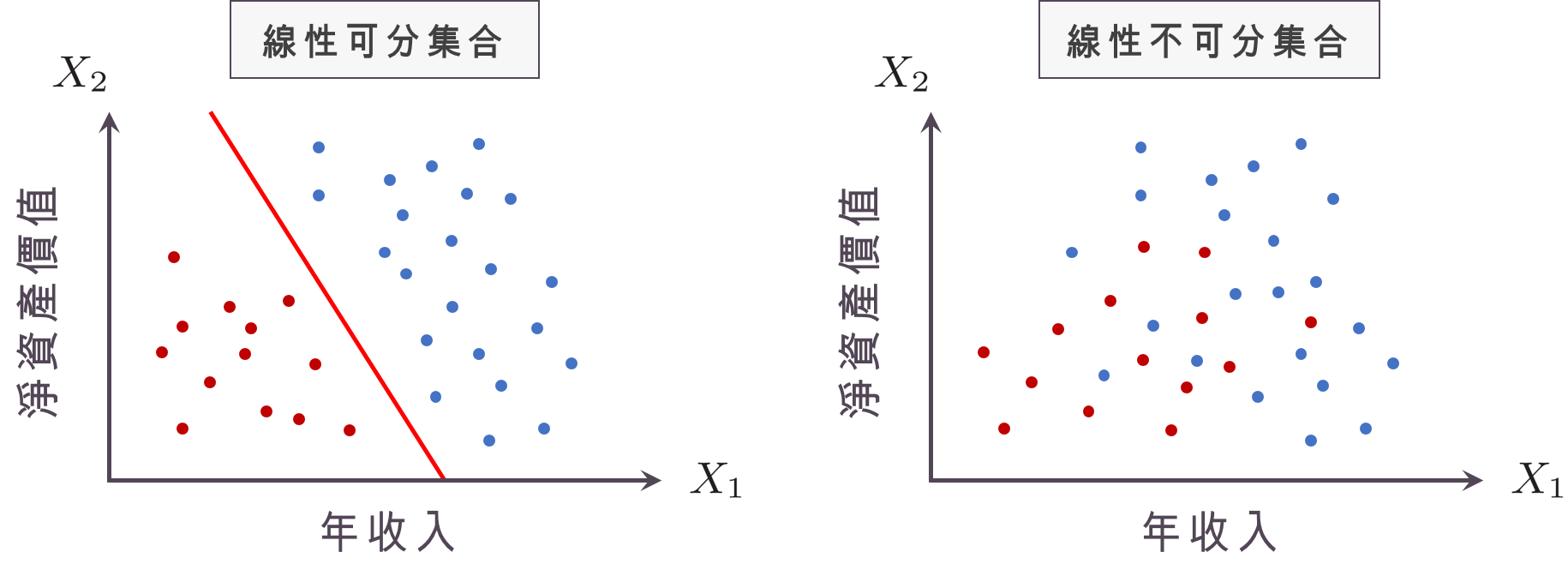
在上左圖中的紅色的線，我們其實可以用數學方程式 $latex  w_1 X_1 + w_2X_2 + b = 0$ 表示，而集合 $latex \{(X_1,X_2): w_1 X_1 + w_2X_2 + b= 0\}$ 則稱為一個「超平面」 (hyperplane)。為什麼是叫做超平面而不是超直線呢？如果我們的有 $latex 3$ 個變數，那麼我們就會用 $latex w_1 X_1 + w_2X_2 + w_3 X_3 + b= 0$ 分開紅色的點與藍色的點，在三維空間中這會形成一個平面，而不是一條線，因此不論變數個數多寡，我們都將這樣的集合稱為「超平面」。

在上左圖線性可分集合的情況，藍色點所落在的紅線右上方區域，其實可以用集合 $latex \{(X_1,X_2): w_1 X_1 + w_2X_2 + b > 0\}$ 表示，而紅色點所在的左下方區域則可以用  $latex \{(X_1,X_2): w_1 X_1 + w_2X_2 + b < 0\}$ 表示，因此對於一個線性可分集合，如果我們可以讓電腦幫我們計算出上左圖紅線的係數 $latex (w_0,w_1,w_2) $，這樣銀行之後有新的 $latex N+1$ 客戶 ，只要蒐集到 $latex (X_{1,N+1}, X_{2,N+1})$ 的資訊，就可以讓電腦自動去判斷客戶會不會違約：

$latex  w_1 X_{1,N+1} +w_2 X_{2,N+1} + b $ 就如同電腦自動幫我們算出來的「違約分數」─
$latex w_1 X_{1,N+1} +w_2 X_{2,N+1} + b< 0$，電腦就會將其分類為「不會違約的客群」，
$latex w_1 X_{1,N+1} +w_2 X_{2,N+1} + b> 0$，電腦就會將其分類為「會違約的客群」。

至於電腦要怎麼樣算出 $latex (w_0,w_1,w_2) $，有兩個常用的演算法：一個是 perceptron learning algorithm，一個是建立在 perceptron learning algorithm 上進行優化的 pocket algorithm，如果對於這兩個演算法有興趣的話，可以在林軒田教授的投影片中找到。

「硬性邊界」 (hard-margin) 的支持向量機

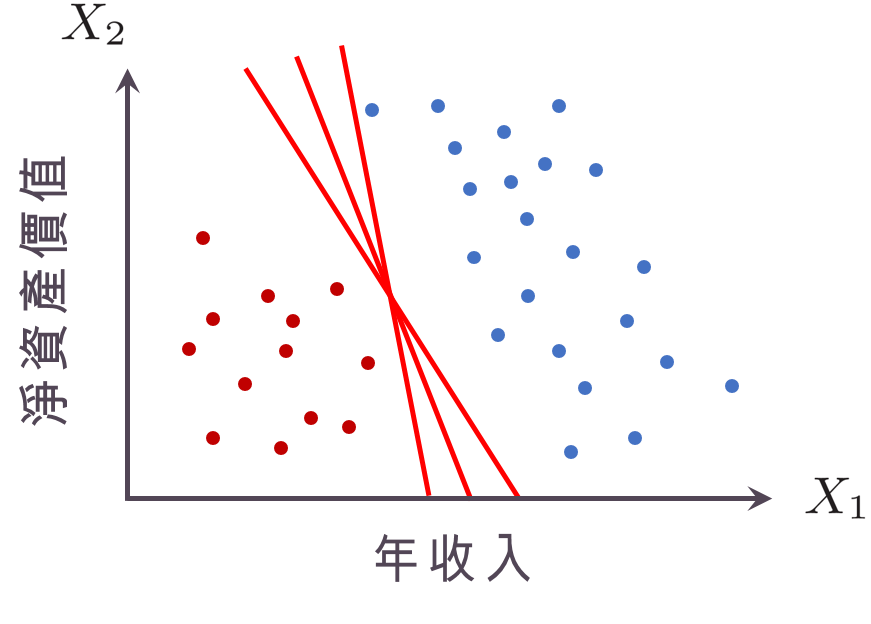
現在，我們將符號稍微化簡一下，令 $latex \mathbf{w} = [w_1~w_2]^T$，$latex \mathbf{x}_i= [X_{1,i}~X_{2,i}]^T$，則之前得到的「超平面」就可以寫成$latex \mathbf{w}^T \mathbf{x} + b = 0$。任何一個可以將藍點與紅點完全分開的平面都叫做「分割超平面」(separating hyperplane)。如果$latex \mathbf{w}^T \mathbf{x} + b = 0$是一個「分割超平面」，那麼電腦在$latex \mathbf{w}^T \mathbf{x} + b > 0$ 時會認為 $latex Y_i = +1$ (符號相同)，$latex \mathbf{w}^T \mathbf{x} + b < 0$ 時會認為$latex Y_i = -1$ (符號相同)，因此對於一個分割超平面而言，對於任意的第$latex i$個樣本，一定會滿足$latex Y_i(\mathbf{w}^T \mathbf{x}_i + b )>0$。對於一個線性可分集合來說，常常會有很多個「分割超平面」，如下圖所示。此時因此一個很自然的問題是：哪一個「分割超平面」最好？

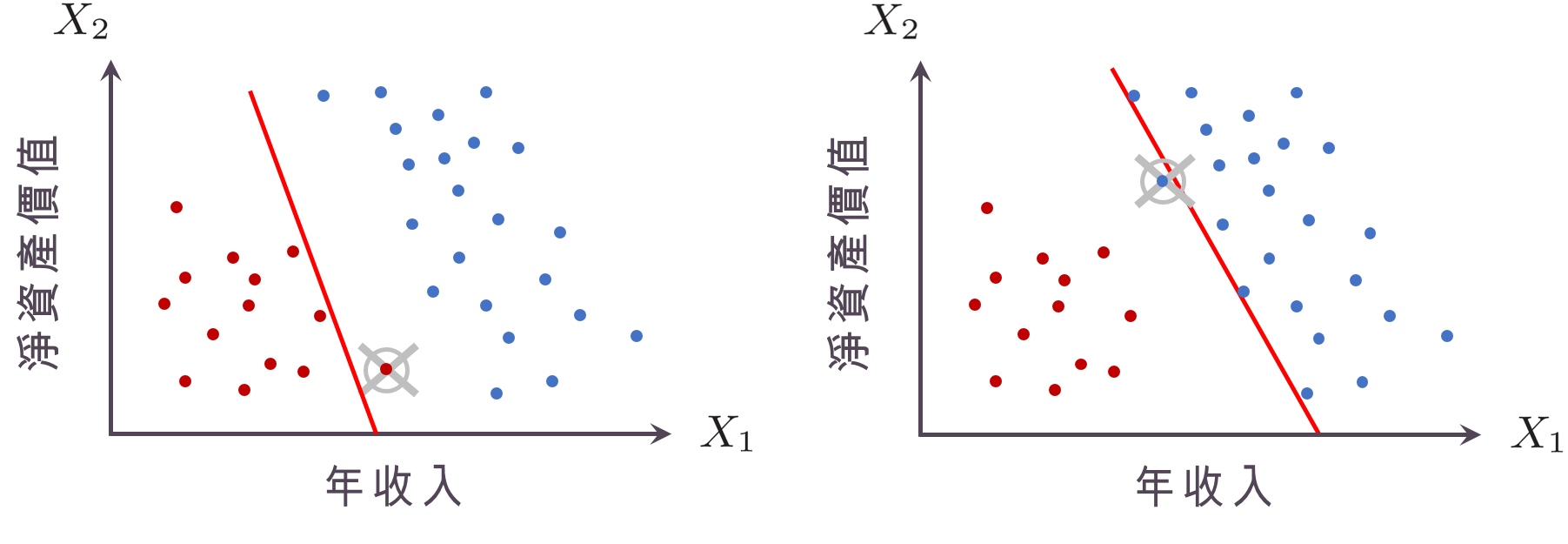
回歸到機器學習本身的目標，是要「準確預測新的個體」，考慮以下兩種「分割超平面」：下左圖的「分割超平面」非常靠近紅色的點，這時如果我們觀察到的新個體只稍微在「分割超平面」的右邊，就會被歸類成藍點，但實際上他跟其他的紅點比起來沒有差很多，應該要是個紅點才對！下右圖的分割超平面非常靠近藍色的點，因此只要稍微往左偏，就會被歸程紅點，這樣會很容易把藍點分錯。因此，真正最好的「分割超平面」，應該是要離兩邊的點都夠遠才好，也就是所謂的「邊距」(margin) 最大。

要怎麼樣讓「邊距」最大呢？之前提到如果對於任意的第$latex i$個樣本，滿足 $latex Y_i(\mathbf{w}^T \mathbf{x}_i + b )>0$ ，就是一個分割超平面，但其實我們也可以把分割的機制寫成：

$latex \mathbf{w}^T \mathbf{x}_i + b > +1$，則認為 $latex Y_i = +1$，
$latex \mathbf{w}^T \mathbf{x}_i + b < -1$ 則認為 $latex Y_i = -1$。

也就是說，我們造出兩個超平面 $latex \mathbf{w}^T \mathbf{x} + b = +1$ 與 $latex \mathbf{w}^T \mathbf{x} + b = -1$，這兩條超平面中間一定會夾著一個「分割超平面」 $latex \mathbf{w}^T \mathbf{x} + b = 0$。此時，這兩個超平面可以用$latex Y_i(\mathbf{w}^T \mathbf{x}_i + b) > 1$ (同號且歸類分數要大於1或小於-1)表示。這兩條超平面之間的距離，就是所謂的「邊距」(margin)，由數學運算可以計算出「邊距」的大小會是 $latex \frac{2}{\|\mathbf{w}\|}$，如下圖所示。這時你可能會想，阿說好的「支持向量」(support vector) 呢？其實我自己更喜歡的名字是maximum margin classifier而不是SVM，而所謂的「支持向量」是剛好落在兩個超平面上的點 $latex \mathbf{X}$，原因是因為：這兩個超平面是由這些點所「支撐」起來的，如下圖兩個紅點撐起了 $latex \mathbf{w}^T \mathbf{x} + b = +1$ ，而兩個藍點撐起了$latex \mathbf{w}^T \mathbf{x} + b = -1$。

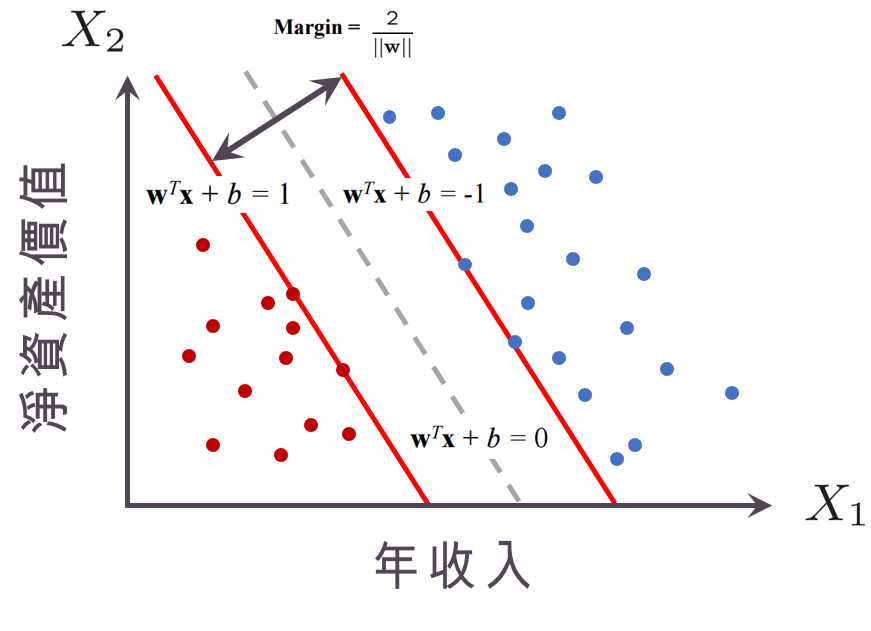
到了這裡，我們就可以把SVM的目標寫出來了！由於「邊距」的大小會是 $latex \frac{2}{\|\mathbf{w}\|}$，因此極大化「邊距」就是極小化$latex \|\mathbf{w}\|$，所以整個SVM就會寫成：

$latex \min_{b,\mathbf{w}} \|\mathbf{w}\|$，受限於 $latex  Y_i(\mathbf{w}^T \mathbf{x}_i + b ) >1$，對於任意的 $latex i = 1,\cdots, N$。

至於這個最佳化問題怎麼解呢？很不幸的，他不是一個可以用微積分以及梯度下降法(gradient descend) 就解出來的問題… 但很幸運的，我們可以透過最佳化理論找出這的問題的對偶型式 (dual form)，然後去解一個Lagrange的極值問題，聽了就頭暈，跳過！上面的方法其實是 SVM 家族裡面最最粗淺的版本，叫做 hard-margin support vector machine。

小結：如果不是線性可分集合怎麼辦？

講了這麼久，我們幾乎都在說線性可分集合，那如果不是線性可分集合怎麼辦呢？聰明的數學家幫我們想好答案了，如果是「非線性可分集合」，我們可以運用核函數(kernel function) 幫我們造出不可分的分割平面，當然核函數就會牽扯到泛涵分析中的「重製核Hilbert空間」(reproducing kernel Hilbert space)，有點麻煩！另外，如果要避免過度配適(over-fitting)的問題，我們也可以讓邊距不要這麼硬派，改用soft-margin SVM，但這也是個麻煩的事情啊！

在這裡大鼻只是簡單的介紹SVM的概念，如果有想知道更多，建議可以看看林軒田老師的投影片喔！希望大鼻有回答道這位讀者的問題……每次寫這麼多數學的文章其實都很害怕大家會被嚇跑，哈哈哈(尷尬) 喜歡大鼻的文章，還要請你們幫我分享跟按讚「大鼻觀點」喔^_^